Introduction

이 글은 의료 영상 진단 기기(예: AI)의 성능을 평가할 때 사용되는 두 가지 핵심 방법론, AFROC와 JAFROC을 비교하고 JAFROC의 원리에 대해 설명합니다.

MRMC 연구란?

MRMC (Multi-Reader, Multi-Case) 연구는 여러 명의 판독자(Multi-Reader)가 여러 개의 증례(Multi-Case)를 보고 진단 성능을 평가하는 연구 설계입니다.

예를 들어, 10명의 영상의학과 의사(판독자)가 100명의 환자(증례) 데이터를 A 방법(예: AI 없음)과 B 방법(예: AI 사용)으로 모두 판독하는 것입니다.

MRMC는 왜 분석이 까다로운가?

MRMC 연구의 목표는 “A 방법과 B 방법 중 어느 것이 더 우수한가?”를 통계적으로 검증하는 것입니다. 하지만 여기에는 여러 변동성(Variability) 요인이 복합적으로 얽혀있습니다.

증례 변동성 (Case Variability): 어떤 증례의 환자 데이터는 진단이 쉽고, 어떤 데이터는 어렵습니다.
독자 변동성 (Reader Variability): 어떤 판독자는 전반적으로 실력이 좋고, 어떤 판독자는 안 좋습니다.
독자-처치 상호작용 (Reader-Treatment Interaction): 어떤 의사는 유독 A 방법(AI 없음)에 익숙하고, 다른 의사는 B 방법(AI 사용)에서만 성능이 크게 향상될 수 있습니다.

올바른 통계 분석은 이 모든 변동성 요인을 고려하여 “평균적으로 B 방법이 A 방법보다 우수하다”고 말할 수 있는지 검증해야 합니다.

MRMC 연구의 성능 평가

진단 성능을 평가하는 지표로 ROC AUC가 널리 쓰입니다. 하지만 이는 증례 당 “정상/비정상” 여부만 판단합니다. 이외에도 LROC, FROC, AFROC, JAFROC 등이 있습니다.

이 글은 ROC와 FROC의 한계를 짚고, AFROC와 JAFROC가 MRMC에서 어떻게 쓰이는지, 그리고 둘의 차이를 설명합니다.

성능 지표: ROC 에서 JAFROC까지지

ROC (Receiver Operating Characteristic)

ROC 분석은 병변 유무(검출) 성능을 평가합니다. 하지만 ROC는 병변의 위치(Localization)를 반영하지 못합니다.

이러한 ROC의 한계를 보완한 분석 곡선이 몇 가지 있습니다.

FROC (Free-Response ROC)

FROC는 병변의 개수에 제약을 두지 않고 평가를 진행한 곡선입니다. 즉, ROC와 다르게 병변 수가 0, 1, 2… 이 될 수 있습니다.

x축: NLF (Non-lesion Localization Fraction) - 이미지당 평균 오탐(비병변 위치 표식) 수 [0, $I n f$ ]

average number of false-positive localizations per image (FP marks per image)
y축: LLF (Lesion Localization Fraction) -병변 단위 민감도 [0,1]

proportion of lesions correctly localized (per-lesion sensitivity)

하지만 FROC의 x축은 상한이 없어 병변의 수에 따라 곡선 범위가 달라집니다.

결과적으로 AUC를 일관되게 정의하고 비교하기 어렵습니다.

AFROC (Alternative Free-Response ROC)

AFROC는 “Free-Response”라는 이름처럼, 한 증례(예: Mammography 이미지 한 장) 안에 여러 개의 병변이 있을 때, 그 병변의 위치까지 올바르게 찾아냈는지를 반영하는 성능 지표입니다.

AFROC는 FROC의 한계를 보완합니다. 마찬가지로 병변의 개수에 제약을 두지 않지만, x축을 다르게 정의하여 [0,1] 범위로 고정시킵니다.

x축: FPF (False Positive Fraction) — 정상 이미지 중 임계값을 넘는 오탐이 하나라도 있는 비율 [0,1]
y축: LLF (Lesion Localization Fraction) — 병변 단위 민감도 [0,1]

두 축이 모두 [0,1] 범위로 고정되므로 AUC 계산이 안정적이고 곡선 간 비교가 용이합니다.

AFROC 곡선의 AUC(곡선 아래 면적)를 FOM (Figure of Merit)이라고 부르며, 이것이 JAFROC 분석에서 사용할 핵심 성능 지표가 됩니다.

JAFROC: AFROC AUC + MRMC 추론 레이어

JAFROC는 AFROC와 동일한 곡선과 동일한 AUC(FOM)를 사용하되, Case-level Jackknife resampling와 OR/ORH형 MRMC분석을 결합해 아래를 제공합니다.

표준오차(SE), 신뢰구간(CI), 유의성 검정(p-value)
상관구조 반영: 같은 독자·다른 처치, 같은 처치·다른 독자, 서로 다른 독자·처치 등 공유 케이스로 인한 공분산 반영

Note

중요: JAFROC는 “새로운 곡선” 이 아닙니다.
AFROC AUC(FOM)는 동일하며, JAFROC는 그 동일한 FOM에 대해
올바른 분산/상관 추정과 MRMC 검정을 얹는 통계적 분석 프레임워크입니다.

AFROC vs. JAFROC (MRMC 관점에서)

MRMC 연구의 목표는 여러 처치(예: A 방법, B 방법)의 진단 성능을 비교하는 것입니다.

가장 단순한 방법은 각 독자/처치별로 AFROC AUC(FOM)를 구한 뒤, 이 점수들을 단순 평균하여 비교하는 것입니다.

하지만 이 ‘단순 평균’ 방식은 MRMC의 핵심 변동성 3가지를 제대로 반영하지 못하며, 이로 인해 표본 오차(SE)를 실제보다 낮게 추정하는 한계가 있습니다.

JAFROC가 필요한 이유: 단순 AFROC의 3가지 한계

AFROC는 아래 3가지 변동성을 무시합니다.

판독자 간 변동성 (Reader Variability)
- 문제점: 어떤 의사는 전반적으로 성능이 높고(예: 항상 90점), 어떤 의사는 낮습니다(예: 항상 70점). 이 ’의사’라는 요인 자체가 거대한 변동성의 원천입니다.
판독자-처치 간 상호작용 (Reader-Treatment Interaction)
- 문제점: A 의사는 1번 처치(AI 없음)에 익숙해 80점을 받았지만, 2번 처치(AI 사용)에는 익숙하지 않아 75점을 받을 수 있습니다. 반면 B 의사는 1번 처치 70점, 2번 처치 85점을 받을 수 있습니다. 이처럼 ’특정 의사’와 ’특정 처치’가 만났을 때 발생하는 변동성을 반영해야 합니다.
증례 유래 공분산 (Case-derived Covariance)
- 문제점: MRMC 연구에서는 ‘같은 독자’가 ‘같은 증례(환자)’를 여러 처치(A, B)로 모두 판독합니다.
- 만약 어떤 증례가 매우 어렵다면(데이터가 안 좋다면), 그 의사는 A 방법에서도 낮은 점수를, B 방법에서도 낮은 점수를 줄 것입니다.
- 이처럼 “같은 증례”를 공유하기 때문에 발생하는 처치 간 점수(FOM)의 상관관계(공분산)를 반드시 고려해야 합니다.

Note

Q: Case-level Bootstrap은 왜 안되나요?

Bootstrap resampling은 (3)번 문제(증례 변동성)는 일부 반영할 수 있지만, (1)번과 (2)번 (판독자 및 판독자-처치 상호작용) 변동성을 제대로 다루지 못합니다. 따라서 여전히 불완전한 방법이며 MRMC의 표준으로 JAFROC를 사용합니다.

JAFROC: 3가지 한계를 모두 해결하는 프레임워크

JAFROC는 이 모든 문제를 해결하기 위해 설계된 통계적 분석 프레임워크입니다.

JAFROC는 AFROC와 동일한 곡선, 동일한 AUC(FOM)를 사용한다는 점이 중요합니다. JAFROC는 그저 이 FOM 점수들을 통계적으로 올바르게 분석하는 ’방법론’의 이름입니다.

[Solution for 3] Case-level Jackknife 방식을 사용하여 증례 유래 공분산을 정확하게 추정합니다.
[Solution for 1, 2] OR/ORH 모델이라는 MRMC 통계 모델을 사용하여 독자 변동성과 독자-처치 상호작용을 모두 반영합니다.

요약

AFROC: 성능 곡선(Plot)과 그 AUC(FOM)라는 ‘성능 지표’를 제공합니다.
JAFROC: AFROC AUC라는 ‘성능 지표’는 그대로 사용하되, Jackknife와 OR/ORH 모델을 결합하여 MRMC의 모든 변동성을 올바르게 반영하는 ‘통계 분석 방법론’입니다.

따라서 JAFROC는 AFROC이 제공하지 못하는 표준오차(SE), 신뢰구간(CI), 그리고 유의성 검정(p-value)을 제공합니다.

JAFROC 작동 원리

JAFROC의 계산 과정은 다음과 같습니다.

(1) Case-level Jackknife Resampling

증례가 K개일 때 처치 i, 판독자 j의 Full FOM $θ_{i j}$ 와 증례 k를 제거한 Delete-1-case FOM $θ_{i j (- k)}$ 를 계산합니다.

Full FOM: ${\hat{θ}}_{i j}$
Delete-1-case FOM: ${\hat{θ}}_{i j (- k)}$ (케이스 $k$ 제거)

다음과 같이 Jackknife Pseudovalue $P_{i j k}$ 를 구합니다.

$P_{i j k} = K {\hat{θ}}_{i j} - (K - 1) {\hat{θ}}_{i j (- k)}$

Delete-1-Case FOM을 계산할 때 증례 k를 제거하면 그 케이스의 모든 병변 마크가 한꺼번에 사라집니다. Jackknife Pseudovalue는 Delete-1-Case FOM을 이용하여 구하기 때문에 $P_{i j k}$ 가 증례 k에 포함된 병변 클러스터 전체의 기여를 반영합니다.

한 증례에 포함된 병변 클러스터가 같이 이동하기 때문에 분산을 구하면 다음과 같이 각 병변의 분산 + 병변–병변 공분산이 포함됩니다.

$Var (\sum_{m = 1}^{L_{k}} ψ (Y_{k, m})) = \sum_{m = 1}^{L_{k}} Var (ψ (Y_{k, m})) + 2 \sum_{1 \leq m < m^{'} \leq L_{k}} Cov (ψ (Y_{k, m}), ψ (Y_{k, m^{'}}))$

즉, 케이스 내 병변-병변 상관(intra-case, intra-lesion correlation)이 자동 반영됩니다.

(2) Case-level jackknife covariance components

Var (same treatment, same reader):
$\hat{Var} \propto \sum_{k = 1}^{K} {\tilde{P}}_{i j k}^{2}$
Cov $_{1}$ (different treatments, same reader):
${\hat{Cov}}_{1} \propto \sum_{i \neq i^{'}} \sum_{k = 1}^{K} {\tilde{P}}_{i j k} {\tilde{P}}_{i^{'} j k}$
Cov $_{2}$ (same treatment, different readers):
${\hat{Cov}}_{2} \propto \sum_{j \neq j^{'}} \sum_{k = 1}^{K} {\tilde{P}}_{i j k} {\tilde{P}}_{i j^{'} k}$
Cov $_{3}$ (different treatments, different readers):
${\hat{Cov}}_{3} \propto \sum_{i \neq i^{'}} \sum_{j \neq j^{'}} \sum_{k = 1}^{K} {\tilde{P}}_{i j k} {\tilde{P}}_{i^{'} j^{'} k}$

(3) OR/ORH(MRMC): 독자 무작위 효과

독자 효과: $R_{j} \sim N (0, σ_{R}^{2})$
독자×처치 효과: $τ R_{i j} \sim N (0, σ_{τ R}^{2})$

OR/ORH는 Obuchowski-Rockette (OR) 모델 (또는 그 확장형인 Hillis(H) 모델)을 의미하며, MRMC 연구 분석을 위해 특별히 설계된 무작위 효과 모델 (Random-Effects Model)입니다.

이 모델이 JAFROC의 핵심인 이유는 앞서 언급한 (1) 독자 간 변동성과 (2) 독자-처치 간 상호작용을 통계적으로 처리하기 때문입니다.

JAFROC는 (1), (2)에서 잭나이프로 얻은 Case level 공분산 성분들( $\hat{Var}, {\hat{Cov}}_{1}, \dots$ )과 (3)의 OR/ORH 모델로 추정한 Reader-level 분산 성분들( $σ_{R}^{2}, σ_{τ R}^{2}$ )을 통계적으로 모두 결합합니다.

이 과정을 통해, 우리가 진짜 알고 싶은 ’독자-평균 처치 차이( $\bar{d}$ )’의 총 분산(Total Variance)을 정확하게 계산해내며, 이를 바탕으로 신뢰할 수 있는 SE, CI, 그리고 F-검정을 제공하는 것입니다.

(4) 최종 가설 검정 및 결론

(1), (2), (3)에서 계산된 분산-공분산 성분과 무작위 효과 모델(OR/ORH)은 MRMC 연구의 핵심 질문에 답하기 위해 사용됩니다.

JAFROC MRMC 분석의 최종 목표는 “여러 처치(Modality) 간에 독자-평균(reader-averaged) 성능(FOM, 즉 AFROC AUC)에 차이가 없다”는 귀무가설(Null Hypothesis)을 검정하는 것입니다.

귀무가설 ( $H_{0}$ ): $μ_{1} = μ_{2} = \dots = μ_{I}$
- (여기서 $μ_{i}$ 는 처치 $i$ 에 대한 모집단의 평균 FOM입니다.)
대립가설 ( $H_{A}$ ): 적어도 하나의 처치에서 평균 FOM이 다릅니다.

(3)에서 언급된 F-검정이 바로 이 귀무가설을 검정합니다. OR/ORH 모델은 (2)에서 잭나이프로 추정한 증례 유래 공분산( ${\hat{Cov}}_{1}, {\hat{Cov}}_{2}, \dots$ )과 (3)의 독자 및 독자-처치 상호작용 변동성( $σ_{R}^{2}, σ_{τ R}^{2}$ )을 모두 반영하여 F-통계량의 분모(오차항)를 구성합니다.

R 코드를 이용한 실습

RJafroc 패키지를 설치하고 불러옵니다.

library(RJafroc)

패키지 안에 있는 dataset01을 불러옵니다.

# MRMC 샘플 데이터(2 처치, 5 독자, 185 증례)
data(dataset01)

UtilFigureOfMerit 함수를 사용하면 개별 FOM(즉, 판독자별 AFROC AUC)을 구할 수 있습니다. 아래는 각 처치(trtBT, trtDM) 별로 각 판독자(rdr)의 AUC 결과입니다.

# dataset01 (2 처치, 5 독자)의 개별 FOM 계산
UtilFigureOfMerit(
  dataset = dataset01,
  FOM = "AFROC"
)

           rdr1      rdr2      rdr3      rdr4      rdr5
trtBT 0.7591557 0.8375000 0.8131031 0.8071272 0.8277961
trtDM 0.6406798 0.7034539 0.7359101 0.7694079 0.6805921

마찬가지로 dataset01 을 불러와서 St 함수를 통해 JAFROC의 최종 F-검정(p-value)을 한 번에 보여줍니다.

# JAFROC MRMC 분석 수행
jafroc_result <- St(
  dataset = dataset01,
  FOM = "AFROC",
  method = "OR" 
)

# 분석 결과(ANOVA 테이블) 출력
# 이 결과에 우리가 찾던 F-검정, p-value가 포함됩니다.
print(jafroc_result)

$FOMs
$FOMs$foms
           rdr1      rdr2      rdr3      rdr4      rdr5
trtBT 0.7591557 0.8375000 0.8131031 0.8071272 0.8277961
trtDM 0.6406798 0.7034539 0.7359101 0.7694079 0.6805921

$FOMs$trtMeans
       Estimate
trtBT 0.8089364
trtDM 0.7060088

$FOMs$trtMeanDiffs
             Estimate
trtBT-trtDM 0.1029276


$ANOVA
$ANOVA$TRanova
            SS DF          MS
T  0.026485243  1 0.026485243
R  0.009461813  4 0.002365453
TR 0.004042448  4 0.001010612

$ANOVA$VarCom
         Estimates      Rhos
VarR  0.0006501141        NA
VarTR 0.0004842873        NA
Cov1  0.0002792523 0.2565054
Cov2  0.0005350491 0.4914658
Cov3  0.0002519457 0.2314231
Var   0.0010886803        NA

$ANOVA$IndividualTrt
      DF   msREachTrt   varEachTrt  cov2EachTrt
trtBT  4 0.0009175795 0.0009568316 0.0005106125
trtDM  4 0.0024584857 0.0012205289 0.0005594856

$ANOVA$IndividualRdr
     DF   msTEachRdr   varEachRdr  cov1EachRdr
rdr1  1 0.0070182667 0.0013828510 0.0001481347
rdr2  1 0.0089841721 0.0009578877 0.0003237347
rdr3  1 0.0029793783 0.0011344453 0.0003160499
rdr4  1 0.0007113727 0.0008835103 0.0002868516
rdr5  1 0.0108345011 0.0010847069 0.0003214908


$RRRC
$RRRC$FTests
                DF          MS    FStat           p
Treatment  1.00000 0.026485243 10.91667 0.003093432
Error     23.05254 0.002426129       NA          NA

$RRRC$ciDiffTrt
             Estimate     StdErr       DF        t       PrGTt    CILower
trtBT-trtDM 0.1029276 0.03115207 23.05254 3.304038 0.003093432 0.03849279
              CIUpper
trtBT-trtDM 0.1673625

$RRRC$ciAvgRdrEachTrt
       Estimate     StdErr       DF   CILower   CIUpper         Cov2
trtBT 0.8089364 0.02634632 57.22585 0.7561833 0.8616895 0.0005106125
trtDM 0.7060088 0.03242195 18.28189 0.6379680 0.7740496 0.0005594856

St 함수는 내부적으로

(1) 각 독자/처치별 FOM 계산 $\to$ (2) Jackknife $\to$ (3) OR/ORH 모델 적용

UtilFigureOfMerit 함수는 이 중 (1)번 단계, 즉 각 독자(Reader)와 처치(Treatment) 조합별 AFROC AUC (FOM) 값( ${\hat{θ}}_{i j}$ )을 직접 계산해서 보여줍니다.

UtilFigureOfMerit(dataset = dataset01, FOM = "AFROC")

           rdr1      rdr2      rdr3      rdr4      rdr5
trtBT 0.7591557 0.8375000 0.8131031 0.8071272 0.8277961
trtDM 0.6406798 0.7034539 0.7359101 0.7694079 0.6805921

jafroc_result$FOMs$foms

           rdr1      rdr2      rdr3      rdr4      rdr5
trtBT 0.7591557 0.8375000 0.8131031 0.8071272 0.8277961
trtDM 0.6406798 0.7034539 0.7359101 0.7694079 0.6805921

UtilFigureOfMerit 함수의 결과와 jafroc_result$FOMs$foms를 비교해보면 값이 똑같습니다. 이를 통해 JAFROC는 AFROC와 똑같은 AUC를 쓴다는 것을 알 수 있습니다.

jafroc_result$FOMs$trtMeans를 통해 전체 AUC는 독자별 AUC의 단순 평균이라는 사실도 알 수 있습니다. 아래 결과입니다.

jafroc_result$FOMs$trtMeans

       Estimate
trtBT 0.8089364
trtDM 0.7060088

jafroc_result$RRRC$FTests가 RRRC (Random Reader, Random Case) 분석 방법에 대한 F-검정 결과를 보여줍니다. 아래 결과입니다.

jafroc_result$RRRC$FTests

                DF          MS    FStat           p
Treatment  1.00000 0.026485243 10.91667 0.003093432
Error     23.05254 0.002426129       NA          NA

Treatment 행의 FStat (10.91667)와 p (0.003093432) 값이 바로 JAFROC 분석법으로 계산한 F-통계량과 p-value입니다.

jafroc_plot <- PlotEmpOpChrs(dataset01, 
              trts = list(1, 2),          # two treatments
              rdrs = list(1:5, 1:5),      # average over all readers for each treatment
              opChType = "AFROC")

jafroc_plot$Plot

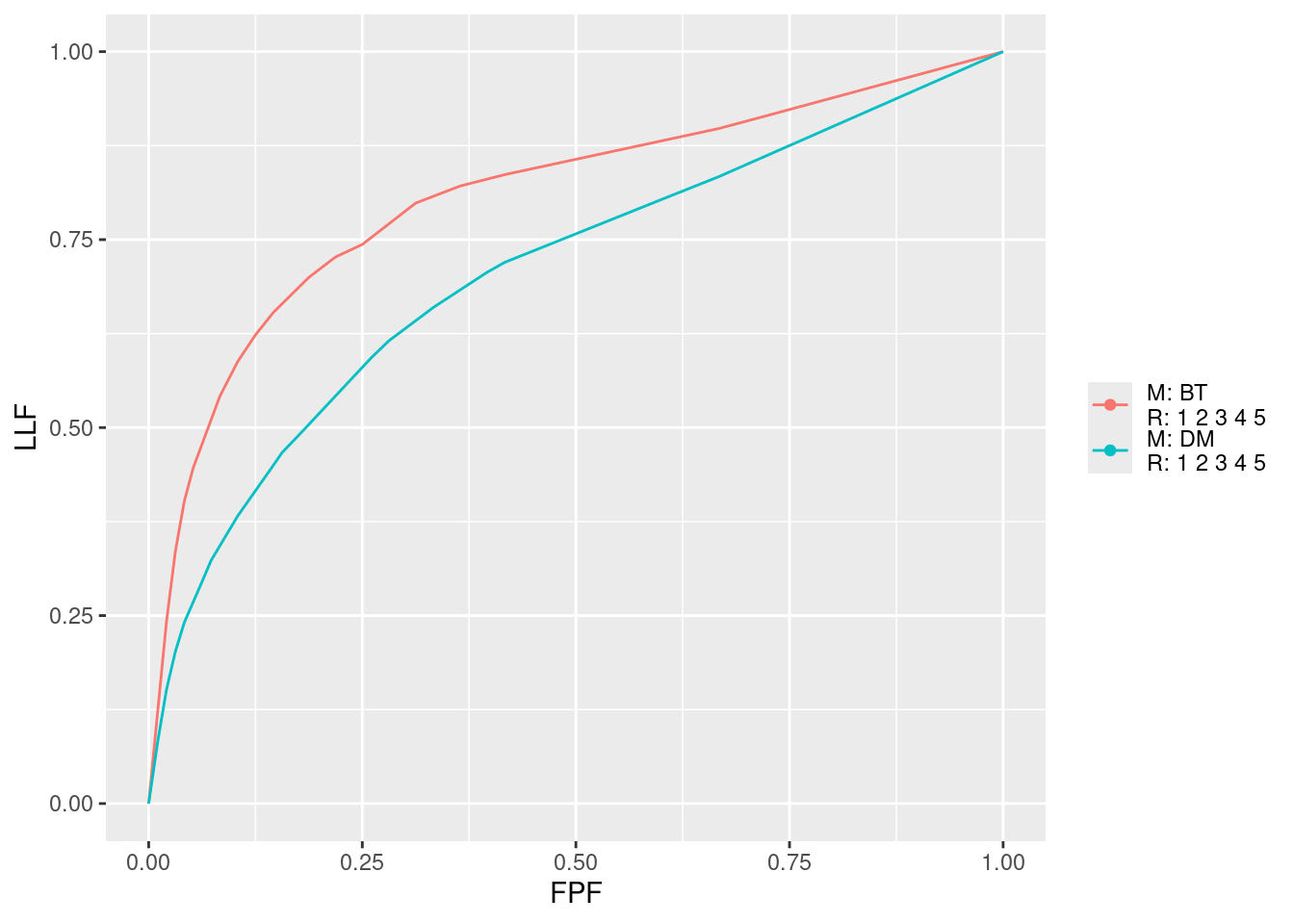
마지막으로 PlotEmpOpChrs 함수를 사용하여 판독자 평균 AFROC 곡선을 그릴 수 있습니다. 위 곡선 2개는 각 trt별 판독자 평균 AFROC 곡선입니다.

trts = list(1, 2)와 rdrs = list(1:5, 1:5)를 지정하면

1번 처치에 대한 5명 독자의 평균 곡선
2번 처치에 대한 5명 독자의 평균 곡선

이렇게 총 2개의 곡선을 비교하여 볼 수 있습니다.

Conclusion

지금까지 AFROC와 JAFROC의 결정적인 차이에 대해 알아봤습니다.

AFROC: 각 판독자의 AUC를 구해 단순 평균을 구할 수 있지만, MRMC의 복잡한 분산 구조(증례, 판독자, 상호작용)를 모두 반영한 통계적 검정(p-value)을 제공하지 못합니다.
JAFROC: AFROC AUC를 성능지표(FOM)로 사용하되, 이를 MRMC의 모든 변동성 요인을 올바르게 고려하는 OR/ORH 통계 프레임워크에 결합합니다.

결론적으로 JAFROC는 증례 내 병변 상관성 (잭나이프로 해결)과 독자 간 변동성 (OR/ORH 모델로 해결)을 모두 적절히 처리하여, 처치 간 성능 차이에 대한 p-value와 신뢰구간(CI)을 제공하는 MRMC 표준 분석법입니다.

Reuse

CC BY-NC 4.0

Citation

BibTeX citation:

@online{hahn2025,
  author = {Hahn, Wonbin},
  title = {AFROC Vs. {JAFROC:} {MRMC} {연구의} {통계} {분석}},
  date = {2025-10-28},
  url = {https://blog.zarathu.com/posts/2025-10-28-jafroc/},
  langid = {en}
}

For attribution, please cite this work as:

Hahn, Wonbin. 2025. “AFROC Vs. JAFROC: MRMC 연구의 통계 분석.” October 28, 2025. https://blog.zarathu.com/posts/2025-10-28-jafroc/.