R 데이터 매니지먼트: 기초

R 기본 문법과, 보험공단 샘플 데이터를 이용한 데이터 매니지먼트 방법을 정리하였습니다. 본 내용은 서울대병원 진단검사의학과 선생님들의 교육에 쓰일 예정입니다.

presentation
lecture
R
Author
Affiliation

Jinseob Kim

Zarathu Co.,Ltd

Published

March 10, 2020

김진섭 대표는 4월 2일(목) 부터 6회에 걸쳐, 서울대병원 진단검사의학과 의국원들의 통계분석 능력 함양을 위한 맞춤 교육 이라는 주제로 R 교육을 진행할 예정입니다. 1주차 강의록을 미리 공유합니다.

시작하기 전에

R 데이터 매니지먼트 방법은 크게 3 종류가 있다.

  1. 원래의 R 문법을 이용한 방법으로 과거 홈페이지1에 정리했었다.

  2. tidyverse는 직관적인 코드를 작성할 수 있는 점을 장점으로 원래의 R 문법을 빠르게 대체하고 있다. 본 블로그에 정리 내용이 있다.

  3. data.table 패키지는 빠른 실행속도를 장점으로 tidyverse 의 득세 속에서 살아남았으며, 역시 과거 홈페이지2에 정리한 바 있다.

본 강의는 이중 첫 번째에 해당하며 2주차에 tidyverse 를 다룰 것이다. data.table 은 이번 교육에는 포함시키지 않았는데, R에 익숙해지면서 느린 속도가 점점 거슬린다면 data.table 을 시작할 때이다.

실습은 클라우드 환경인 RStudio cloud 를 이용하여 진행한다. 회원가입 후, 아래를 따라 강의자료가 포함된 실습환경을 생성하자.

  1. https://rstudio.cloud 회원 가입
  1. https://rstudio.cloud/spaces/53975/join?access_code=kuFNlbt%2FbSj6DH%2FuppMdXzvU4e1EPrQNgNsFAQBf 들어가서 “Join Space” 클릭
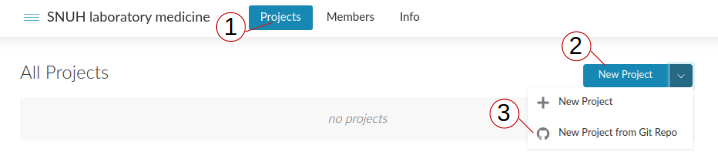
  1. 위쪽 “Projects” 클릭 후, “New Project” 를 눌러 “New Project from Git Repo” 를 선택 후, Repo 주소 https://github.com/jinseob2kim/lecture-snuhlab 입력.

project 생성

개인 PC에서 실습을 원한다면 http://www.r-project.org 와 https://rstudio.com/products/rstudio/download/#download 에서 R과 RStudio 를 설치하자.

전체 강의 일정

회차 일시 주제
1 4월 2일(목) 11-13시 R 데이터 매니지먼트 기초
2 4월 14일(화) 11-13시 R 데이터 매니지먼트 최근: tidyverse
3 4월 28일(화) 11-13시 R 데이터 시각화: ggplot2
4 5월 12일(화) 11-13시 의학연구에서의 기술통계
5 5월 26일(화) 11-13시 회귀분석, 생존분석
6 6월 9일(화) 11-13시 R로 논문쓰기: rmarkdown

R 기초연산 : 벡터(vector)

R 의 기본 연산단위는 벡터이며, x <- c(1, 2, 3) 은 1,2,3 으로 이루어진 길이 3인 벡터를 x 에 저장한다. 대입연산자는 = 와 <- 둘 다 가능하지만 함수의 인자로도 쓰이는 = 와 구별하기 위해 <- 를 권장한다. 자주 쓰는 연산을 실습하자.

x <- c(1, 2, 3, 4, 5, 6)            ## vector of variable
y <- c(7, 8, 9, 10, 11, 12)
x + y                                  
[1]  8 10 12 14 16 18
x * y
[1]  7 16 27 40 55 72
sqrt(x)                            ## root
[1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490
sum(x)                                
[1] 21
diff(x)                            ## difference
[1] 1 1 1 1 1
mean(x)                            ## mean  
[1] 3.5
var(x)                             ## variance
[1] 3.5
sd(x)                              ## standard deviation
[1] 1.870829
median(x)                          ## median
[1] 3.5
IQR(x)                             ## inter-quantile range
[1] 2.5
max(x)                             ## max value
[1] 6
which.max(x)                       ## order of max value
[1] 6
max(x, y)                          ## max value among x & y
[1] 12
length(x)                          
[1] 6

max(x, y) 는 x, y 각각의 최대값이 아닌, 전체에서 최대인 값 1개를 보여줌을 기억하자. 잠시 후 각각의 최대값 구하는 연습문제가 나온다.

벡터에서 특정 항목을 골라내려면 그것의 위치 혹은 조건문을 이용한다.

x[2]                               ## 2 번째
[1] 2
x[-2]                              ## 2 번째만 빼고
[1] 1 3 4 5 6
x[1:3]                             ## 1-3 번째
[1] 1 2 3
x[c(1, 2, 3)]                      ## 동일 
[1] 1 2 3
x[c(1, 3, 4, 5, 6)]                ## 1, 3, 4, 5, 6  번째
[1] 1 3 4 5 6
x >= 4                             ## 각 항목이 4 이상인지 TRUE/FALSE
[1] FALSE FALSE FALSE  TRUE  TRUE  TRUE
sum(x >= 4)                        ## TRUE 1, FALSE 0 인식 
[1] 3
x[x >= 4]                          ## TRUE 인 것들만, 즉 4 이상인 것들         
[1] 4 5 6
sum(x[x >= 4])                     ## 4 이상인 것들만 더하기. 
[1] 15
x %in% c(1, 3, 5)                  ## 1, 3, 5 중 하나에 속하는지 TRUE/FALSE
[1]  TRUE FALSE  TRUE FALSE  TRUE FALSE
x[x %in% c(1, 3, 5)]               
[1] 1 3 5

벡터만들기

seq 로 일정 간격인, rep 로 항목들이 반복되는 벡터를 만들 수 있다.

v1 <- seq(-5, 5, by = .2); v1             ## Sequence
 [1] -5.0 -4.8 -4.6 -4.4 -4.2 -4.0 -3.8 -3.6 -3.4 -3.2 -3.0 -2.8 -2.6 -2.4 -2.2
[16] -2.0 -1.8 -1.6 -1.4 -1.2 -1.0 -0.8 -0.6 -0.4 -0.2  0.0  0.2  0.4  0.6  0.8
[31]  1.0  1.2  1.4  1.6  1.8  2.0  2.2  2.4  2.6  2.8  3.0  3.2  3.4  3.6  3.8
[46]  4.0  4.2  4.4  4.6  4.8  5.0
v2 <- rep(1, 3); v2                       ## Repeat
[1] 1 1 1
v3 <- rep(c(1, 2, 3), 2); v3              ## Repeat for vector
[1] 1 2 3 1 2 3
v4 <- rep(c(1, 2, 3), each = 2); v4       ## Repeat for vector : each
[1] 1 1 2 2 3 3

for, if/else, ifelse 문

for loop 는 같은 작업을 반복할 때 이용하며 while 도 비슷한 의미이다. 예시를 통해 배워보자.

for (i in 1:3){
  print(i)
}
[1] 1
[1] 2
[1] 3
i <- 0
for (j in c(1, 2, 4, 5, 6)){
  i <- i + j
}
i
[1] 18

if 와 else 는 조건문을 다룬다. else 나 else if 문은 선행 조건문의 마지막과 같은 줄이어야 함을 기억하자.

x <- 5
if (x >= 3 ){
  x <- x + 3
}
x
[1] 8
x <- 5
if (x >= 10){
  print("High")
} else if (x >= 5){
  print("Medium")
} else {
  print("Low")
}                                          ## else if, else 주의: 반드시 } 와 같은 줄에 위치하도록.
[1] "Medium"

ifelse 는 벡터화된 if/else 문으로 벡터의 각 항목마다 조건문을 적용하는데, 엑셀의 if 문과 비슷하다.

x <- 1:6
y <- ifelse(x >= 4, "Yes", "No")           ## ifelse (조건,참일때,거짓일때)
y
[1] "No"  "No"  "No"  "Yes" "Yes" "Yes"

함수 만들기

막 R을 배우는 단계에서는 함수를 만들어 쓸 일이 거의 없겠지만, 결측치 포함된 데이터에서 평균이나 분산을 구할 때 귀찮을 수 있다. R은 결측치가 하나라도 포함되면 평균값, 분산값으로 NA를 출력하기 때문이다. 이를 해결하기 위해서라도 아래처럼 기초 함수 만드는 법은 알고 있는 것이 좋다.

x <- c(1:10, 12, 13, NA, NA, 15, 17)      ## 결측치가 포함되어 있다면..
mean(x)                                           
[1] NA
mean0 <- function(x){
  mean(x, na.rm = T)
}                                         ## mean함수의 na.rm 옵션을 TRUE로 바꿈. default는 F

mean0 <- function(x){mean(x, na.rm = T)}  ## 한줄에 쓸 수도 있다. 
mean0(x)
[1] 8

둘 이상의 변수를 포함한 함수도 다음과 같이 만들 수 있다.

twomean <- function(x1, x2){
  a <- (x1 + x2)/2
  a
}
twomean(4, 6)
[1] 5

Apply 문 : apply, sapply, lapply

벡터를 다루는 연산을 잘 활용하면, 벡터의 각 항목에 대해 for loop 을 쓰는 것보다 간편하게 코드를 작성할 수 있다. 행렬에서 행마다 평균을 구하는 예를 살펴보자.

mat <- matrix(1:20, nrow = 4, byrow = T)   ## 4행 5열, byrow = T : 행부터 채운다. 
mat
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    2    3    4    5
[2,]    6    7    8    9   10
[3,]   11   12   13   14   15
[4,]   16   17   18   19   20

모든 행에 대해 for loop 을 이용, 평균을 구하여 저장하는 코드는 아래와 같다.

out <- NULL                                ## 빈 벡터, 여기에 하나씩 붙여넣는다.
for (i in 1:nrow(mat)){
  out <- c(out, mean(mat[i, ]))
}
out
[1]  3  8 13 18

처음에 빈 벡터를 만들고 여기에 결과를 붙여가는 모습이 번거로워 보인다. sapply 또는 lapply 를 사용하면 행 또는 열 단위 연산을 간단히 수행할 수 있다.

sapply(1:nrow(mat), function(x){mean(mat[x, ])})             ## Return vector
[1]  3  8 13 18
lapply(1:nrow(mat), function(x){mean(mat[x, ])})             ## Return list type
[[1]]
[1] 3

[[2]]
[1] 8

[[3]]
[1] 13

[[4]]
[1] 18
unlist(lapply(1:nrow(mat), function(x){mean(mat[x, ])}))     ## Same to sapply
[1]  3  8 13 18

처음에 빈 벡터를 만들고, 이어붙이는 과정이 생략되어 간단한 코드가 되었다. list 는 벡터보다 상위개념으로 모든 것을 담을 수 있는 큰 그릇에 비유할 수 있는데, 본 강의에서는 unlist 를 취하면 벡터나 행렬을 얻게 된다는 정도만 언급하고 넘어가겠다. 사실 행렬의 행/열 단위 연산은 apply 혹은 row***, col*** 시리즈의 함수가 따로 있어, 더 간단히 이용할 수 있다.

apply(mat, 1, mean)                                          ## 1: 행
[1]  3  8 13 18
rowMeans(mat)                                                ## 동일
[1]  3  8 13 18
rowSums(mat)                                                 ## 행별로 합
[1] 15 40 65 90
apply(mat, 2, mean)                                          ## 2: 열
[1]  8.5  9.5 10.5 11.5 12.5
colMeans(mat)                                                ## 열별로 합
[1]  8.5  9.5 10.5 11.5 12.5

연습문제 1

sapply나 lapply를 이용하여, 아래 두 벡터의 최대값을 각각 구하여라.

x <- 1:6
y <- 7:12
정답 보기 
lapply(list(x, y), max)
[[1]]
[1] 6

[[2]]
[1] 12
  sapply(list(x, y), max)
[1]  6 12


멀티코어 병렬연산으로 apply 를 빠르게 수행할 수도 있는데 본 강의에서는 생략한다. 궁금하신 분은 과거 정리 내용 을 참고하기 바란다.

데이터 불러와서 작업하기

이제부터는 실제 데이터를 읽어서 그 데이터를 매니징 하는 방법을 배워보도록 하겠다.

데이터 불러오기, 저장하기

데이터를 불러오기 전에 미리 디렉토리를 지정하면 그 다음부터는 편하게 읽고 쓸 수 있다.

getwd()                                                     ## 현재 디렉토리 
setwd("data")                                               ## 디렉토리 설정
## 동일
setwd("/home/js/Homepage/blog/_posts/2020-02-16-rdatamanagement-basic/data")
getwd()

폴더 구분을 / 로 해야 한다는 점을 명심하자 (\\ 도 가능). R 은 유닉스 기반이기 때문이다. 이제 실습 데이터를 읽어볼텐데, 가급적이면 데이터 포맷은 csv로 만드는 것을 추천한다. 콤마로 분리된 가장 간단한 형태로, 용량도 작고 어떤 소프트웨어 에서도 읽을 수 있기 때문이다. 물론 Excel, SPSS, SAS 파일도 읽을 수 있는데, 변수명이나 값에 한글이 있으면 encoding 에러가 생길 수 있으므로 미리 처리하자.

ex <- read.csv("example_g1e.csv")
head(ex)

URL 링크를 이용할 수도 있다.

ex <- read.csv("https://raw.githubusercontent.com/jinseob2kim/lecture-snuhlab/master/data/example_g1e.csv")

Excel 파일은 readxl, SAS나 SPSS는 haven 패키지를 이용한다.

#install.packages(c("readxl", "haven"))                    ## install packages    
library(readxl)                                            ## for xlsx
ex.excel <- read_excel("example_g1e.xlsx", sheet = 1)      ## 1st sheet

library(haven)                                             ## for SAS/SPSS/STATA   
ex.sas <- read_sas("example_g1e.sas7bdat")                 ## SAS
ex.spss <- read_sav("example_g1e.sav")                     ## SPSS
head(ex.spss)

아래와 같이 Excel, SAS, SPSS 데이터는 read.csv 와 형태가 좀 달라보인다. 이것은 최근 R에서 인기있는 tidyverse 스타일의 데이터인데, 자세한 내용은 다음 강의에서 다룰 예정이니 일단 넘어가자.

파일 저장은 write.csv 를 이용하며, 맨 왼쪽에 나타나는 행 넘버링을 빼려면 row.names = F 옵션을 추가한다.

write.csv(ex, "example_g1e_ex.csv", row.names = F)

haven 패키지에서 write_sas 나 write_sav 도 가능하다.

write_sas(ex.sas, "example_g1e_ex.sas7bdat")
write_sav(ex.spss, "example_g1e_ex.sav")

읽은 데이터 살펴보기

본격적으로 데이터를 살펴보자. 데이터는 09-15년 공단 건강검진 데이터에서 실습용으로 32 명을 뽑은 자료이며, 자세한 내용은 “data/2교시 테이블 세부 레이아웃 소개(최신자료).pdf” 를 참고하자.

데이터 살펴보기

head 로 처음 6줄, tail 로 마지막 6줄을 볼 수 있다. 데이터 간단히 확인하려고 쓰인다.

head(ex)                                                   ## 처음 6행
tail(ex)                                                   ## 마지막 6행
head(ex, 10)                                               ## 처음 10행

str 은 head 와는 다른 방식으로 데이터를 확인한다. int 는 정수, num 은 실수형을 의미한다.

str(ex)
'data.frame':   1644 obs. of  32 variables:
 $ EXMD_BZ_YYYY  : int  2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 ...
 $ RN_INDI       : int  562083 334536 911867 183321 942671 979358 554112 487160 793017 219397 ...
 $ HME_YYYYMM    : int  200909 200911 200903 200908 200909 200912 200911 200908 200906 200912 ...
 $ Q_PHX_DX_STK  : int  0 0 0 NA NA NA NA NA NA 0 ...
 $ Q_PHX_DX_HTDZ : int  0 0 0 NA NA NA NA NA NA 0 ...
 $ Q_PHX_DX_HTN  : int  1 0 0 NA NA NA NA NA NA 1 ...
 $ Q_PHX_DX_DM   : int  0 0 0 NA NA NA NA NA NA 0 ...
 $ Q_PHX_DX_DLD  : int  0 0 0 NA NA NA NA NA NA 0 ...
 $ Q_PHX_DX_PTB  : int  NA NA NA NA NA NA NA NA NA NA ...
 $ Q_HBV_AG      : int  3 2 3 3 3 2 2 3 3 3 ...
 $ Q_SMK_YN      : int  1 1 1 1 1 1 1 1 1 1 ...
 $ Q_DRK_FRQ_V09N: int  0 0 0 0 0 0 0 0 0 0 ...
 $ HGHT          : int  144 162 163 152 159 157 160 159 156 146 ...
 $ WGHT          : int  61 51 65 51 50 55 56 54 53 48 ...
 $ WSTC          : int  90 63 82 70 73 73 67 66 67 78 ...
 $ BMI           : num  29.4 19.4 24.5 22.1 19.8 22.3 21.9 21.4 21.8 22.5 ...
 $ VA_LT         : num  0.7 0.8 0.7 0.8 0.7 1.5 1.5 1.2 1.2 1.5 ...
 $ VA_RT         : num  0.8 1 0.6 0.9 0.8 1.5 1.5 1.5 1 1.5 ...
 $ BP_SYS        : int  120 120 130 101 132 110 119 111 138 138 ...
 $ BP_DIA        : int  80 80 80 62 78 70 78 60 72 84 ...
 $ URN_PROT      : int  1 1 1 1 1 1 1 1 1 1 ...
 $ HGB           : num  12.6 13.8 15 13.1 13 11.9 11.2 12.2 11 12.8 ...
 $ FBS           : int  117 96 118 90 92 100 84 88 74 107 ...
 $ TOT_CHOL      : int  264 169 216 199 162 192 152 166 155 178 ...
 $ TG            : int  128 92 132 100 58 109 38 42 86 87 ...
 $ HDL           : int  60 70 55 65 40 53 43 58 52 35 ...
 $ LDL           : int  179 80 134 114 111 117 101 99 85 125 ...
 $ CRTN          : num  0.9 0.9 0.8 0.9 0.9 0.7 0.8 1 0.6 0.7 ...
 $ SGOT          : int  25 18 26 18 24 15 8 16 15 21 ...
 $ SGPT          : int  20 15 30 14 23 12 6 11 13 21 ...
 $ GGT           : int  25 28 30 11 15 14 10 12 13 23 ...
 $ GFR           : int  59 74 79 61 49 83 97 65 96 70 ...

names 로 변수들 이름을 확인할 수 있다. 공백이나 특수문자는 “.” 로 바뀌고, 이름이 같은 변수들은 뒤에 숫자가 추가되어 구별된다. read.csv(..., check.names = F) 옵션으로 원래 이름을 유지할 수 있으나 에러의 원인이 되므로 추천하지 않는다.

names(ex)
 [1] "EXMD_BZ_YYYY"   "RN_INDI"        "HME_YYYYMM"     "Q_PHX_DX_STK"  
 [5] "Q_PHX_DX_HTDZ"  "Q_PHX_DX_HTN"   "Q_PHX_DX_DM"    "Q_PHX_DX_DLD"  
 [9] "Q_PHX_DX_PTB"   "Q_HBV_AG"       "Q_SMK_YN"       "Q_DRK_FRQ_V09N"
[13] "HGHT"           "WGHT"           "WSTC"           "BMI"           
[17] "VA_LT"          "VA_RT"          "BP_SYS"         "BP_DIA"        
[21] "URN_PROT"       "HGB"            "FBS"            "TOT_CHOL"      
[25] "TG"             "HDL"            "LDL"            "CRTN"          
[29] "SGOT"           "SGPT"           "GGT"            "GFR"

샘플수, 변수 갯수는 dim, nrow, ncol 로 확인한다.

dim(ex)                                                    ## row, column
[1] 1644   32
nrow(ex)                                                   ## row
[1] 1644
ncol(ex)                                                   ## column
[1] 32

클래스는 class로 확인한다. read.csv 는 data.frame, Excel/SAS/SPSS 는 tibble & `data.frame 인데, data.frame 은 행렬이면서 데이터에 특화된 list, tibble 은 앞서 언급했던 tidyverse 스타일의 data.frame 인 정도만 알고 넘어가자.

class(ex)
[1] "data.frame"
class(ex.spss)
[1] "tbl_df"     "tbl"        "data.frame"

summary 로 모든 변수들의 평균, 중위수, 결측치 등을 한 번에 확인할 수 있다. R은 결측치를 NA 로 표시하며, 안타깝지만 분산은 나오지 않는다.

  EXMD_BZ_YYYY     RN_INDI          HME_YYYYMM      Q_PHX_DX_STK   
 Min.   :2009   Min.   :   2270   Min.   :200901   Min.   :0.0000  
 1st Qu.:2010   1st Qu.: 230726   1st Qu.:201011   1st Qu.:0.0000  
 Median :2012   Median : 487160   Median :201210   Median :0.0000  
 Mean   :2012   Mean   : 490782   Mean   :201216   Mean   :0.0112  
 3rd Qu.:2014   3rd Qu.: 726101   3rd Qu.:201406   3rd Qu.:0.0000  
 Max.   :2015   Max.   :1010623   Max.   :201512   Max.   :1.0000  
                                                   NA's   :573     
 Q_PHX_DX_HTDZ     Q_PHX_DX_HTN   Q_PHX_DX_DM      Q_PHX_DX_DLD   
 Min.   :0.0000   Min.   :0.00   Min.   :0.0000   Min.   :0.0000  
 1st Qu.:0.0000   1st Qu.:0.00   1st Qu.:0.0000   1st Qu.:0.0000  
 Median :0.0000   Median :0.00   Median :0.0000   Median :0.0000  
 Mean   :0.0241   Mean   :0.25   Mean   :0.0693   Mean   :0.0399  
 3rd Qu.:0.0000   3rd Qu.:0.25   3rd Qu.:0.0000   3rd Qu.:0.0000  
 Max.   :1.0000   Max.   :1.00   Max.   :1.0000   Max.   :1.0000  
 NA's   :566      NA's   :492    NA's   :547      NA's   :566     
  Q_PHX_DX_PTB       Q_HBV_AG        Q_SMK_YN     Q_DRK_FRQ_V09N 
 Min.   :0.0000   Min.   :1.000   Min.   :1.000   Min.   :0.000  
 1st Qu.:0.0000   1st Qu.:2.000   1st Qu.:1.000   1st Qu.:0.000  
 Median :0.0000   Median :2.000   Median :1.000   Median :1.000  
 Mean   :0.0276   Mean   :2.235   Mean   :1.632   Mean   :1.026  
 3rd Qu.:0.0000   3rd Qu.:3.000   3rd Qu.:2.000   3rd Qu.:2.000  
 Max.   :1.0000   Max.   :3.000   Max.   :3.000   Max.   :7.000  
 NA's   :703      NA's   :2       NA's   :2       NA's   :6      
      HGHT            WGHT            WSTC             BMI       
 Min.   :134.0   Min.   : 31.0   Min.   : 57.00   Min.   :12.30  
 1st Qu.:158.0   1st Qu.: 56.0   1st Qu.: 74.00   1st Qu.:21.50  
 Median :165.0   Median : 64.0   Median : 81.00   Median :23.70  
 Mean   :164.5   Mean   : 65.1   Mean   : 80.69   Mean   :23.92  
 3rd Qu.:171.0   3rd Qu.: 73.0   3rd Qu.: 87.00   3rd Qu.:26.20  
 Max.   :188.0   Max.   :118.0   Max.   :114.00   Max.   :37.20  
                                                                 
     VA_LT           VA_RT            BP_SYS          BP_DIA     
 Min.   :0.100   Min.   :0.1000   Min.   : 81.0   Min.   : 49.0  
 1st Qu.:0.800   1st Qu.:0.7000   1st Qu.:110.0   1st Qu.: 70.0  
 Median :1.000   Median :1.0000   Median :120.0   Median : 78.0  
 Mean   :0.984   Mean   :0.9792   Mean   :122.3   Mean   : 76.6  
 3rd Qu.:1.200   3rd Qu.:1.2000   3rd Qu.:130.0   3rd Qu.: 82.0  
 Max.   :9.900   Max.   :9.9000   Max.   :180.0   Max.   :120.0  
                                                                 
    URN_PROT          HGB             FBS            TOT_CHOL    
 Min.   :1.000   Min.   : 5.90   Min.   : 61.00   Min.   : 68.0  
 1st Qu.:1.000   1st Qu.:12.90   1st Qu.: 86.00   1st Qu.:170.0  
 Median :1.000   Median :14.10   Median : 94.00   Median :193.0  
 Mean   :1.078   Mean   :14.11   Mean   : 97.23   Mean   :194.9  
 3rd Qu.:1.000   3rd Qu.:15.40   3rd Qu.:103.00   3rd Qu.:218.0  
 Max.   :5.000   Max.   :18.30   Max.   :290.00   Max.   :363.0  
 NA's   :4                                                       
       TG              HDL             LDL              CRTN        
 Min.   :  13.0   Min.   : 23.0   Min.   :  19.0   Min.   : 0.4000  
 1st Qu.:  72.0   1st Qu.: 46.0   1st Qu.:  90.0   1st Qu.: 0.8000  
 Median : 106.0   Median : 54.0   Median : 112.0   Median : 0.9000  
 Mean   : 134.9   Mean   : 55.9   Mean   : 118.7   Mean   : 0.9891  
 3rd Qu.: 163.0   3rd Qu.: 64.0   3rd Qu.: 134.0   3rd Qu.: 1.0000  
 Max.   :1210.0   Max.   :593.0   Max.   :8100.0   Max.   :16.5000  
                                  NA's   :16                        
      SGOT            SGPT             GGT              GFR        
 Min.   :  6.0   Min.   :  3.00   Min.   :  6.00   Min.   :  3.00  
 1st Qu.: 19.0   1st Qu.: 15.00   1st Qu.: 16.00   1st Qu.: 76.00  
 Median : 23.0   Median : 20.00   Median : 24.50   Median : 87.00  
 Mean   : 25.6   Mean   : 25.98   Mean   : 36.34   Mean   : 89.74  
 3rd Qu.: 28.0   3rd Qu.: 30.00   3rd Qu.: 41.00   3rd Qu.:101.00  
 Max.   :459.0   Max.   :779.00   Max.   :408.00   Max.   :196.00  
                                                   NA's   :467

특정 변수 보기

data.frame 에서 특정변수는 $ 를 이용, 데이터이름$변수이름 로 확인할 수 있다. 앞서 언급했듯이 data.frame 은 행렬과 list의 성질도 갖고 있어 해당 스타일로도 가능하다.

ex$EXMD_BZ_YYYY                                            ## data.frame style
ex[, "EXMD_BZ_YYYY"]                                       ## matrix style
ex[["EXMD_BZ_YYYY"]]                                       ## list style
ex[, 1]                                                    ## matrix style with order
ex[[1]]                                                    ## list style with order

2개 이상 변수선택은 행렬 스타일을 이용한다.

ex[, c("EXMD_BZ_YYYY", "RN_INDI", "BMI")]                  ## matrix syle with names
ex[, c(1, 2, 16)]                                          ## matrix syle with names
ex[, names(ex)[c(1, 2, 16)]]                               ## same

특정 변수는 벡터형태로 나타나므로 처음에 다루었던 벡터다루기를 그대로 활용할 수 있다. 예를 들어 년도 변수인 EXMD_BZ_YYYY의 첫 50개만 확인하면 아래와 같다.

ex$EXMD_BZ_YYYY[1:50]                                      ## data.frame style
ex[1:50, 1]                                                ## matrix style
ex[[1]][1:50]                                              ## list style
 [1] 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009
[16] 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009
[31] 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009 2009
[46] 2009 2009 2009 2009 2009

unique 로 변수가 어떤 값들로 이루어져 있는지, table 로 해당 값들이 몇개씩 있는지 확인한다.

unique(ex$EXMD_BZ_YYYY)                                   ## unique value
[1] 2009 2010 2011 2012 2013 2014 2015
length(unique(ex$EXMD_BZ_YYYY))                           ## number of unique value
[1] 7
table(ex$EXMD_BZ_YYYY)                                    ## table

2009 2010 2011 2012 2013 2014 2015 
 214  236  223  234  243  254  240

새로운 변수 만들기

연속형 변수인 BMI 에서 원하는 조건에 맞는 정보를 뽑아내는 연습을 해 보자.

mean(ex$BMI)                                              ## mean
[1] 23.92257
BMI_cat <- (ex$BMI >= 25)                                 ## TRUE of FALSE
table(BMI_cat)                         
BMI_cat
FALSE  TRUE 
 1077   567 
rows <- which(ex$BMI >= 25)                               ## row numbers
head(rows)                                      
[1]  1 14 18 21 23 24
values <- ex$BMI[ex$BMI >= 25]                            ## values
head(values)
[1] 29.4 27.5 27.7 28.0 30.7 25.6
length(values)
[1] 567
BMI_HGHT_and <- (ex$BMI >= 25 & ex$HGHT >= 175)              ## and
BMI_HGHT_or <- (ex$BMI >= 25 | ex$HGHT >= 175)               ## or

데이터에 새로운 변수로 추가하는 방법은 간단하다.

ex$zero <- 0                                              ## variable with 0
ex$BMI_cat <- (ex$BMI >= 25)                              ## T/F
ex$BMI_cat <- as.integer(ex$BMI >= 25)                    ## 0, 1
ex$BMI_cat <- as.character(ex$BMI >= 25)                  ## "0", "1"
ex$BMI_cat <- ifelse(ex$BMI >= 25, "1", "0")              ## same
table(ex$BMI_cat)

   0    1 
1077  567 
ex[, "BMI_cat"] <- (ex$BMI >= 25)                         ## matrix style
ex[["BMI_cat"]] <- (ex$BMI >= 25)                         ## list style

변수 클래스 설정: 데이터 읽은 후 가장 먼저 해야할 것.

앞서 데이터의 클래스가 data.frame 임을 언급했었는데, 각 변수들도 자신의 클래스를 갖으며 대표적인 것이 숫자형(numeric), 문자형(character), 팩터(factor) 이다. 그 외 T/F 로 나타내는 논리(logical), 날짜를 나타내는 Date 클래스가 있다. 숫자는 integer(정수), numeric(실수) 이 있는데, 전부 실수형(numeric)으로 해도 상관없어 설명은 생략한다. 범주형은 character 와 factor 두 종류가 있는데, 전자는 단순 문자인 반면 후자는 레벨(level) 이 있어 reference 나 순서를 설정할 수 있다. read.csv 로 읽으면 숫자는 int/num, 문자는 전부 factor 가 기본값이므로, 숫자 변수 중 0/1 같은 것들은 직접 factor 로 바꿔줘야 한다. ID와 설문조사 변수를 범주형으로 바꿔보자.

vars.cat <- c("RN_INDI", "Q_PHX_DX_STK", "Q_PHX_DX_HTDZ", "Q_PHX_DX_HTN", "Q_PHX_DX_DM", "Q_PHX_DX_DLD", "Q_PHX_DX_PTB", 
              "Q_HBV_AG", "Q_SMK_YN", "Q_DRK_FRQ_V09N")
vars.cat <- names(ex)[c(2, 4:12)]                              ## same
vars.cat <- c("RN_INDI", grep("Q_", names(ex), value = T))     ## same: extract variables starting with "Q_"

vars.conti <- setdiff(names(ex), vars.cat)                     ## Exclude categorical variables
vars.conti <- names(ex)[!(names(ex) %in% vars.cat)]            ## same: !- not, %in%- including

for (vn in vars.cat){                                          ## for loop: as.factor
  ex[, vn] <- as.factor(ex[, vn])
}

for (vn in vars.conti){                                        ## for loop: as.numeric
  ex[, vn] <- as.numeric(ex[, vn])
}

summary(ex)
  EXMD_BZ_YYYY     RN_INDI       HME_YYYYMM     Q_PHX_DX_STK Q_PHX_DX_HTDZ
 Min.   :2009   4263   :   7   Min.   :200901   0   :1059    0   :1052    
 1st Qu.:2010   38967  :   7   1st Qu.:201011   1   :  12    1   :  26    
 Median :2012   56250  :   7   Median :201210   NA's: 573    NA's: 566    
 Mean   :2012   84322  :   7   Mean   :201216                             
 3rd Qu.:2014   99917  :   7   3rd Qu.:201406                             
 Max.   :2015   115809 :   7   Max.   :201512                             
                (Other):1602                                              
 Q_PHX_DX_HTN Q_PHX_DX_DM Q_PHX_DX_DLD Q_PHX_DX_PTB Q_HBV_AG    Q_SMK_YN  
 0   :864     0   :1021   0   :1035    0   :915     1   :  77   1   :995  
 1   :288     1   :  76   1   :  43    1   : 26     2   :1102   2   :256  
 NA's:492     NA's: 547   NA's: 566    NA's:703     3   : 463   3   :391  
                                                    NA's:   2   NA's:  2  
                                                                          
                                                                          
                                                                          
 Q_DRK_FRQ_V09N      HGHT            WGHT            WSTC       
 0      :805    Min.   :134.0   Min.   : 31.0   Min.   : 57.00  
 1      :379    1st Qu.:158.0   1st Qu.: 56.0   1st Qu.: 74.00  
 2      :249    Median :165.0   Median : 64.0   Median : 81.00  
 3      :121    Mean   :164.5   Mean   : 65.1   Mean   : 80.69  
 4      : 28    3rd Qu.:171.0   3rd Qu.: 73.0   3rd Qu.: 87.00  
 (Other): 56    Max.   :188.0   Max.   :118.0   Max.   :114.00  
 NA's   :  6                                                    
      BMI            VA_LT           VA_RT            BP_SYS     
 Min.   :12.30   Min.   :0.100   Min.   :0.1000   Min.   : 81.0  
 1st Qu.:21.50   1st Qu.:0.800   1st Qu.:0.7000   1st Qu.:110.0  
 Median :23.70   Median :1.000   Median :1.0000   Median :120.0  
 Mean   :23.92   Mean   :0.984   Mean   :0.9792   Mean   :122.3  
 3rd Qu.:26.20   3rd Qu.:1.200   3rd Qu.:1.2000   3rd Qu.:130.0  
 Max.   :37.20   Max.   :9.900   Max.   :9.9000   Max.   :180.0  
                                                                 
     BP_DIA         URN_PROT          HGB             FBS        
 Min.   : 49.0   Min.   :1.000   Min.   : 5.90   Min.   : 61.00  
 1st Qu.: 70.0   1st Qu.:1.000   1st Qu.:12.90   1st Qu.: 86.00  
 Median : 78.0   Median :1.000   Median :14.10   Median : 94.00  
 Mean   : 76.6   Mean   :1.078   Mean   :14.11   Mean   : 97.23  
 3rd Qu.: 82.0   3rd Qu.:1.000   3rd Qu.:15.40   3rd Qu.:103.00  
 Max.   :120.0   Max.   :5.000   Max.   :18.30   Max.   :290.00  
                 NA's   :4                                       
    TOT_CHOL           TG              HDL             LDL        
 Min.   : 68.0   Min.   :  13.0   Min.   : 23.0   Min.   :  19.0  
 1st Qu.:170.0   1st Qu.:  72.0   1st Qu.: 46.0   1st Qu.:  90.0  
 Median :193.0   Median : 106.0   Median : 54.0   Median : 112.0  
 Mean   :194.9   Mean   : 134.9   Mean   : 55.9   Mean   : 118.7  
 3rd Qu.:218.0   3rd Qu.: 163.0   3rd Qu.: 64.0   3rd Qu.: 134.0  
 Max.   :363.0   Max.   :1210.0   Max.   :593.0   Max.   :8100.0  
                                                  NA's   :16      
      CRTN              SGOT            SGPT             GGT        
 Min.   : 0.4000   Min.   :  6.0   Min.   :  3.00   Min.   :  6.00  
 1st Qu.: 0.8000   1st Qu.: 19.0   1st Qu.: 15.00   1st Qu.: 16.00  
 Median : 0.9000   Median : 23.0   Median : 20.00   Median : 24.50  
 Mean   : 0.9891   Mean   : 25.6   Mean   : 25.98   Mean   : 36.34  
 3rd Qu.: 1.0000   3rd Qu.: 28.0   3rd Qu.: 30.00   3rd Qu.: 41.00  
 Max.   :16.5000   Max.   :459.0   Max.   :779.00   Max.   :408.00  
                                                                    
      GFR              zero      BMI_cat      
 Min.   :  3.00   Min.   :0   Min.   :0.0000  
 1st Qu.: 76.00   1st Qu.:0   1st Qu.:0.0000  
 Median : 87.00   Median :0   Median :0.0000  
 Mean   : 89.74   Mean   :0   Mean   :0.3449  
 3rd Qu.:101.00   3rd Qu.:0   3rd Qu.:1.0000  
 Max.   :196.00   Max.   :0   Max.   :1.0000  
 NA's   :467

summary 를 보면 설문조사 변수들이 처음과 달리 빈도로 요약됨을 알 수 있다. 한 가지 주의할 점은 factor 를 numeric 으로 바로 바꾸면 안된다는 것이다. 방금 factor 로 바꾼 Q_PHX_DX_STK 를 numeric 으로 바꿔서 테이블로 요약하면, 원래의 0/1 이 아닌 1/2로 바뀐다.

table(
  as.numeric(ex$Q_PHX_DX_STK)
  )

   1    2 
1059   12

factor를 바로 바꾸면 원래 값이 아닌, factor에 내장된 레벨(순서값) 로 바뀌기 때문이다. 제대로 바꾸려면 아래처럼 character 로 먼저 바꿔준 후 숫자형을 적용해야 한다.

table(
  as.numeric(as.character(ex$Q_PHX_DX_STK))
  )

   0    1 
1059   12

마지막으로 Date 클래스를 살펴보자. 검진년월 변수인 HME_YYYYMM 를 Date 로 바꿔 볼텐데, Date는 년/월/일 이 모두 필요하므로 일은 1로 통일하고 paste 로 붙이겠다.

addDate <- paste(ex$HME_YYYYMM, "01", sep = "")                ## add day- use `paste`
ex$HME_YYYYMM <- as.Date(addDate, format = "%Y%m%d")           ## set format                  
head(ex$HME_YYYYMM)
[1] "2009-09-01" "2009-11-01" "2009-03-01" "2009-08-01" "2009-09-01"
[6] "2009-12-01"
class(ex$HME_YYYYMM)
[1] "Date"

결측치 다루기

변수 클래스만큼 중요한 것이 결측치 처리이다. 앞서 “함수만들기” 에서 봤듯이 결측치가 있으면 평균같은 기본적인 계산도 na.rm = T 옵션이 필요하다. 결측치가 있는 LDL 변수의 평균을 연도별로 구해보자. 그룹별 통계는 tapply 를 이용한다.

tapply(ex$LDL, ex$EXMD_BZ_YYYY, mean)                          ## measure/group/function
2009 2010 2011 2012 2013 2014 2015
150.9486 NA NA NA NA NA NA

2009년만 결측치가 없고, 나머지는 결측치가 있어 평균값이 NA 로 나온다.na.rm = T 옵션으로 결측치를 제외하면 원하는 결과를 얻는다.

tapply(ex$LDL, ex$EXMD_BZ_YYYY, 
       function(x){
         mean(x, na.rm = T)
         })    
    2009     2010     2011     2012     2013     2014     2015 
150.9486 112.9914 112.9450 117.5259 111.1577 116.5455 111.5294

더 큰 문제는, 대부분의 R 통계분석이 결측치를 갖는 샘플을 분석에서 제외한다는 점이다. 그래서 결측치를 신경쓰지 않고 분석하다보면, 원래 샘플 수와 분석에 이용된 샘플 수가 달라지는 문제가 생길 수 있다. LDL과 HDL 의 회귀분석 결과를 예로 살펴보자.

summary(lm(LDL ~ HDL, data = ex))

Call:
lm(formula = LDL ~ HDL, data = ex)

Residuals:
   Min     1Q Median     3Q    Max 
-103.8  -28.2   -6.6   15.4 7974.7 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 138.2747    15.2318   9.078   <2e-16 ***
HDL          -0.3499     0.2570  -1.362    0.174    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 201.9 on 1626 degrees of freedom
  (16 observations deleted due to missingness)
Multiple R-squared:  0.001139,  Adjusted R-squared:  0.0005244 
F-statistic: 1.854 on 1 and 1626 DF,  p-value: 0.1735

“16 observations deleted due to missingness” 라는 글자가 보일 것이다. LDL 이 결측인 16명은 분석에서 제외했다는 뜻이다.

연습문제 2: 결측치 처리

결측치를 처리하는 제일 간단한 방법은 “하나라도 결측치 있는 샘플은 제외” 로, na.omit 함수를 이용하면 된다.

ex.naomit <- na.omit(ex)
nrow(ex.naomit)
[1] 620

1644 명에서 620 명으로 샘플 수가 줄어든 것을 확인할 수 있다. 필자는 보통 결측치 처리에 다음의 3가지 원칙을 적용한다.

  1. 결측치 너무 많으면(예: 10% 이상) 그 변수는 삭제

  2. 연속변수는 중간값(median)

  3. 범주형변수는 최빈값(mode)

이제 문제이다. 아까 변수형을 정리한 ex 데이터에 위 3가지 원칙을 적용, 새로운 데이터 ex.impute 을 만들어 보아라. 단 최빈값 함수는 아래와 같이 getmode 로 주어진다.

getmode <- function(v){
   uniqv <- unique(v)
   uniqv[which.max(tabulate(match(v, uniqv)))]
}

getmode(ex$Q_PHX_DX_STK)
[1] 0
Levels: 0 1
정답 보기 
vars.ok <- sapply(names(ex), function(v){sum(is.na(ex[, v])) < nrow(ex)/10})
ex.impute <- ex[, vars.ok]                                     ## only missing < 10%

for (v in names(ex.impute)){
  if (is.factor(ex.impute[, v])){                              ## or class(ex[, v]) == "factor"
    ex.impute[, v] <- ifelse(is.na(ex.impute[, v]), 
                             getmode(ex.impute[, v]), 
                             ex.impute[, v])
  } else if (is.numeric(ex[, v])){                             ## or class(ex[, v]) %in% c("integer", "numeric")
    ex.impute[, v] <- ifelse(is.na(ex.impute[, v]), 
                             median(ex.impute[, v], na.rm = T), 
                             ex.impute[, v])
  } else{                                                      ## when date
    ex.impute[, v]
  }
}

summary(ex.impute)
  EXMD_BZ_YYYY     RN_INDI        HME_YYYYMM            Q_HBV_AG    
 Min.   :2009   Min.   :  1.0   Min.   :2009-01-01   Min.   :1.000  
 1st Qu.:2010   1st Qu.:133.8   1st Qu.:2010-11-01   1st Qu.:2.000  
 Median :2012   Median :275.0   Median :2012-10-01   Median :2.000  
 Mean   :2012   Mean   :272.7   Mean   :2012-08-31   Mean   :2.235  
 3rd Qu.:2014   3rd Qu.:405.2   3rd Qu.:2014-06-01   3rd Qu.:3.000  
 Max.   :2015   Max.   :547.0   Max.   :2015-12-01   Max.   :3.000  
    Q_SMK_YN     Q_DRK_FRQ_V09N       HGHT            WGHT      
 Min.   :1.000   Min.   :1.000   Min.   :134.0   Min.   : 31.0  
 1st Qu.:1.000   1st Qu.:1.000   1st Qu.:158.0   1st Qu.: 56.0  
 Median :1.000   Median :2.000   Median :165.0   Median : 64.0  
 Mean   :1.631   Mean   :2.023   Mean   :164.5   Mean   : 65.1  
 3rd Qu.:2.000   3rd Qu.:3.000   3rd Qu.:171.0   3rd Qu.: 73.0  
 Max.   :3.000   Max.   :8.000   Max.   :188.0   Max.   :118.0  
      WSTC             BMI            VA_LT           VA_RT       
 Min.   : 57.00   Min.   :12.30   Min.   :0.100   Min.   :0.1000  
 1st Qu.: 74.00   1st Qu.:21.50   1st Qu.:0.800   1st Qu.:0.7000  
 Median : 81.00   Median :23.70   Median :1.000   Median :1.0000  
 Mean   : 80.69   Mean   :23.92   Mean   :0.984   Mean   :0.9792  
 3rd Qu.: 87.00   3rd Qu.:26.20   3rd Qu.:1.200   3rd Qu.:1.2000  
 Max.   :114.00   Max.   :37.20   Max.   :9.900   Max.   :9.9000  
     BP_SYS          BP_DIA         URN_PROT          HGB       
 Min.   : 81.0   Min.   : 49.0   Min.   :1.000   Min.   : 5.90  
 1st Qu.:110.0   1st Qu.: 70.0   1st Qu.:1.000   1st Qu.:12.90  
 Median :120.0   Median : 78.0   Median :1.000   Median :14.10  
 Mean   :122.3   Mean   : 76.6   Mean   :1.078   Mean   :14.11  
 3rd Qu.:130.0   3rd Qu.: 82.0   3rd Qu.:1.000   3rd Qu.:15.40  
 Max.   :180.0   Max.   :120.0   Max.   :5.000   Max.   :18.30  
      FBS            TOT_CHOL           TG              HDL       
 Min.   : 61.00   Min.   : 68.0   Min.   :  13.0   Min.   : 23.0  
 1st Qu.: 86.00   1st Qu.:170.0   1st Qu.:  72.0   1st Qu.: 46.0  
 Median : 94.00   Median :193.0   Median : 106.0   Median : 54.0  
 Mean   : 97.23   Mean   :194.9   Mean   : 134.9   Mean   : 55.9  
 3rd Qu.:103.00   3rd Qu.:218.0   3rd Qu.: 163.0   3rd Qu.: 64.0  
 Max.   :290.00   Max.   :363.0   Max.   :1210.0   Max.   :593.0  
      LDL              CRTN              SGOT            SGPT       
 Min.   :  19.0   Min.   : 0.4000   Min.   :  6.0   Min.   :  3.00  
 1st Qu.:  90.0   1st Qu.: 0.8000   1st Qu.: 19.0   1st Qu.: 15.00  
 Median : 112.0   Median : 0.9000   Median : 23.0   Median : 20.00  
 Mean   : 118.6   Mean   : 0.9891   Mean   : 25.6   Mean   : 25.98  
 3rd Qu.: 134.0   3rd Qu.: 1.0000   3rd Qu.: 28.0   3rd Qu.: 30.00  
 Max.   :8100.0   Max.   :16.5000   Max.   :459.0   Max.   :779.00  
      GGT              zero      BMI_cat      
 Min.   :  6.00   Min.   :0   Min.   :0.0000  
 1st Qu.: 16.00   1st Qu.:0   1st Qu.:0.0000  
 Median : 24.50   Median :0   Median :0.0000  
 Mean   : 36.34   Mean   :0   Mean   :0.3449  
 3rd Qu.: 41.00   3rd Qu.:0   3rd Qu.:1.0000  
 Max.   :408.00   Max.   :0   Max.   :1.0000


Subset

특정 조건을 만족하는 서브데이터는 지금까지 배웠던 것을 응용해 만들 수도 있지만, subset 함수가 편하다. 아래는 2012 이후의 자료만 뽑는 예시이다. 이제부터는 결측치를 전부 제외한 ex.naomit 데이터를 이용하겠다.

ex1 <- ex.naomit                                               ## simple name
ex1.2012 <- ex1[ex1$EXMD_BZ_YYYY >= 2012, ]
table(ex1.2012$EXMD_BZ_YYYY)

2012 2013 2014 2015 
 151  162  154  153 
ex1.2012 <- subset(ex1, EXMD_BZ_YYYY >= 2012)                  ## subset
table(ex1.2012$EXMD_BZ_YYYY)

2012 2013 2014 2015 
 151  162  154  153

그룹별 통계

결측치 다루기에서 그룹별 통계를 구할 때 tapply 를 이용했었다. tapply 를 여러 변수, 여러 그룹을 동시에 고려도록 확장할 수 있는 함수가 aggregate 로, 허리둘레와 BMI의 평균을 고혈압 또는 당뇨 여부에 따라 살펴보자.

aggregate(ex1[, c("WSTC", "BMI")], list(ex1$Q_PHX_DX_HTN), mean)
aggregate(cbind(WSTC, BMI) ~ Q_PHX_DX_HTN, data = ex1, mean)   ## same
Group.1 WSTC BMI
0 80.35687 23.85592
1 84.48958 25.11771
Q_PHX_DX_HTN WSTC BMI
0 80.35687 23.85592
1 84.48958 25.11771

결측치가 있어도 잘 적용된다는 장점이 있다.

aggregate(cbind(WSTC, BMI) ~ Q_PHX_DX_HTN, data = ex, mean)
Q_PHX_DX_HTN WSTC BMI
0 80.23958 23.70961
1 83.87847 24.99861

당뇨여부도 그룹으로 다루려면 list 에 추가하면 된다.

aggregate(ex1[, c("WSTC", "BMI")], list(ex1$Q_PHX_DX_HTN, ex1$Q_PHX_DX_DM), mean)
Group.1 Group.2 WSTC BMI
0 0 80.23107 23.82990
1 0 83.93976 25.17952
0 1 87.55556 25.34444
1 1 88.00000 24.72308

Group.1 이 첫번째 그룹은 고혈압 여부, Group.2 가 두번째 그룹인 당뇨 여부이다. 위와 마찬가지로 formula 형태를 이용할 수도 있다.

aggregate(cbind(WSTC, BMI) ~ Q_PHX_DX_HTN + Q_PHX_DX_DM, data = ex1, mean)
Q_PHX_DX_HTN Q_PHX_DX_DM WSTC BMI
0 0 80.23107 23.82990
1 0 83.93976 25.17952
0 1 87.55556 25.34444
1 1 88.00000 24.72308

표준편차를 같이 보려면 function(x){c(mean = mean(x), sd = sd(x))} 와 같이 원하는 함수들을 벡터로 모으면 된다.

aggregate(cbind(WSTC, BMI) ~ Q_PHX_DX_HTN + Q_PHX_DX_DM, data = ex1, function(x){c(mean = mean(x), sd = sd(x))})
Warning in `[<-.data.frame`(`*tmp*`, , isn, value = structure(list(WSTC.mean =
c("80.231068", : provided 4 variables to replace 2 variables
Q_PHX_DX_HTN Q_PHX_DX_DM WSTC BMI
0 0 80.231068 9.546884
1 0 83.939759 9.124277
0 1 87.555556 7.551674
1 1 88.000000 6.177918

아예 데이터의 모든 변수의 평균을 다 볼순 없을까? 아래처럼 “.” 으로 전체 데이터를 지정할 수 있다.

aggregate(. ~ Q_PHX_DX_HTN  + Q_PHX_DX_DM, data = ex1, function(x){c(mean = mean(x), sd = sd(x))})    
  Q_PHX_DX_HTN Q_PHX_DX_DM EXMD_BZ_YYYY.mean EXMD_BZ_YYYY.sd RN_INDI.mean
1            0           0       2013.493204        1.109498    269.30680
2            1           0       2013.578313        1.105645    251.78313
3            0           1       2013.333333        1.414214    269.77778
4            1           1       2013.307692        1.031553    303.53846
  RN_INDI.sd HME_YYYYMM.mean HME_YYYYMM.sd Q_PHX_DX_STK.mean Q_PHX_DX_STK.sd
1  159.12594      16102.3184      422.8574        1.00776699      0.08787296
2  154.03951      16121.8072      413.1641        1.01204819      0.10976426
3   92.88807      16036.3333      551.2248        1.00000000      0.00000000
4  142.18686      16018.6923      417.4666        1.07692308      0.27735010
  Q_PHX_DX_HTDZ.mean Q_PHX_DX_HTDZ.sd Q_PHX_DX_DLD.mean Q_PHX_DX_DLD.sd
1         1.00194175       0.04406526         1.0174757       0.1311630
2         1.06024096       0.23937916         1.0722892       0.2605404
3         1.00000000       0.00000000         1.0000000       0.0000000
4         1.07692308       0.27735010         1.0769231       0.2773501
  Q_PHX_DX_PTB.mean Q_PHX_DX_PTB.sd Q_HBV_AG.mean Q_HBV_AG.sd Q_SMK_YN.mean
1         1.0271845       0.1627787     2.2291262   0.5236863     1.6970874
2         1.0000000       0.0000000     2.1927711   0.5512255     1.3855422
3         1.0000000       0.0000000     2.0000000   0.0000000     1.6666667
4         1.0769231       0.2773501     2.2307692   0.4385290     1.5384615
  Q_SMK_YN.sd Q_DRK_FRQ_V09N.mean Q_DRK_FRQ_V09N.sd  HGHT.mean    HGHT.sd
1   0.8674234           2.0388350         1.3329287 166.613592   9.116636
2   0.6777172           1.9759036         1.3612754 160.506024   9.254364
3   0.8660254           1.8888889         0.3333333 168.333333  10.185774
4   0.6602253           1.9230769         1.1151636 162.384615   9.639662
  WGHT.mean   WGHT.sd WSTC.mean   WSTC.sd  BMI.mean    BMI.sd VA_LT.mean
1 66.582524 13.211630 80.231068  9.546884 23.829903  3.276315  1.0190291
2 65.313253 13.155661 83.939759  9.124277 25.179518  3.693922  0.8469880
3 71.777778  8.913161 87.555556  7.551674 25.344444  2.711140  0.9111111
4 65.076923  6.211032 88.000000  6.177918 24.723077  2.057164  0.7769231
   VA_LT.sd VA_RT.mean  VA_RT.sd BP_SYS.mean  BP_SYS.sd BP_DIA.mean BP_DIA.sd
1 0.5248189  1.0079612 0.3503677  119.889320  13.378266   75.452427  9.464616
2 0.3201895  0.8638554 0.3444962  132.879518  14.344539   81.481928 11.015910
3 0.1691482  0.8111111 0.2368778  128.555556   8.647415   83.333333 11.842719
4 0.2350668  0.9000000 0.1080123  129.461538  12.149180   79.307692  7.846280
  URN_PROT.mean URN_PROT.sd   HGB.mean     HGB.sd  FBS.mean    FBS.sd
1     1.0543689   0.3430173 14.3749515  1.5952305  94.75534  12.71807
2     1.2168675   0.6634756 14.1048193  1.6682036 103.60241  14.34330
3     1.0000000   0.0000000 15.2555556  1.0284832 131.11111  19.62425
4     1.0769231   0.2773501 13.4153846  0.9711215 125.30769  34.11838
  TOT_CHOL.mean TOT_CHOL.sd   TG.mean     TG.sd  HDL.mean    HDL.sd  LDL.mean
1     196.96505    34.20684 132.80777 107.56421 54.943689 12.881333 118.49903
2     191.30120    32.64769 138.09639  81.93106 55.903614 16.123468 108.22892
3     169.77778    47.79325 164.66667  68.40870 46.333333  9.394147  92.77778
4     179.61538    39.92397 154.76923 139.23072 48.769231 10.288779 102.30769
     LDL.sd CRTN.mean   CRTN.sd SGOT.mean   SGOT.sd SGPT.mean   SGPT.sd
1  50.86475 0.8871845 0.1867988 24.151456  9.426161 24.609709 16.616090
2  29.09167 0.9168675 0.2483208 25.289157  6.400324 22.963855  9.671993
3  38.88694 0.9666667 0.2549510 35.777778 25.849457 47.666667 44.235167
4  28.39420 0.9153846 0.1675617 31.769231 19.689904 36.307692 27.417709
  GGT.mean   GGT.sd GFR.mean   GFR.sd zero.mean zero.sd BMI_cat.mean BMI_cat.sd
1 34.47573 31.35216 92.01359 19.14246         0       0    0.3223301  0.4678230
2 35.77108 31.18799 81.16867 17.75430         0       0    0.4337349  0.4986022
3 44.22222 21.01058 87.55556 22.20423         0       0    0.5555556  0.5270463
4 48.46154 66.83265 80.69231 14.34332         0       0    0.1538462  0.3755338

Sort

정렬은 순위함수인 order 를 이용한다. 기본은 오름차순이며, 내림차순을 원한다면 (-) 붙인 값의 순위를 구하면 된다.

ord <- order(ex1$HGHT)                                        ## 작은 순서대로 순위
head(ord)
[1] 500 168   3 328 473 177
head(ex1$HGHT[ord])                                           ## Sort
[1] 138 139 140 140 141 143
ord.desc <- order(-ex1$HGHT)                                  ## descending
head(ex1$HGHT[ord.desc])
[1] 188 186 185 185 184 183
ex1.sort <- ex1[ord, ]
head(ex1.sort)

Wide to long, long to wide format

받은 데이터가 원하는 형태가 아닌 경우가 있다. 수축기 혈압을 10번 측정해서 각각 SBP1, SBP2, …, SBP10 변수에 기록된 데이터를 본다면, 이것들을 쫙 아래로 내려 측정시기, 측정값 2개의 변수로 정리하고 싶다는 마음이 들 것이다. 이럴 때 쓰는 함수가 melt, 반대로 데이터를 옆으로 늘릴 때 쓰는 함수가 dcast 이다(Figure @ref(fig:melt)3).

melt and dcast

실습으로 수축기/이완기 혈압 변수를 합쳐서 아래로 내려보자.

library(reshape2)
long <- melt(ex1, id = c("EXMD_BZ_YYYY", "RN_INDI"), measure.vars = c("BP_SYS", "BP_DIA"), variable.name = "BP_type", value.name = "BP")
long

id 는 유지할 변수, measure.vars 는 내릴 변수를 의미하고, variable.name, value.name 은 각각 그룹, 값의 변수이름을 의미한다. 이를 원래대로 되돌리려면 dcast 를 이용하는데, “유지할 변수 ~ 펼칠 변수” 형태로 formula 를 입력한다.

wide <- dcast(long, EXMD_BZ_YYYY + RN_INDI ~ BP_type, value.var = "BP")
head(wide)

Merge

merge 함수를 이용한다. “by” 옵션으로 기준이 되는 공통 컬럼을 설정하며, 기준 컬럼의 이름이 두 데이터 셋에서 다른 경우는 “by.x” 와 “by.y” 로 따로 설정한다. 실습을 위해 ex1 데이터를 2개로 나눈 후 merge 를 적용하겠다.

ex1.Q <- ex1[, c(1:3, 4:12)]
ex1.measure <- ex1[, c(1:3, 13:ncol(ex1))]
head(ex1.Q)
head(ex1.measure)

전자는 설문조사 결과를, 후자는 측정값을 포함했고 “년도, ID, 검진년월” 은 공통변수이다. 이 공통변수로 merge 를 적용하면

ex1.merge <- merge(ex1.Q, ex1.measure, by = c("EXMD_BZ_YYYY", "RN_INDI", "HME_YYYYMM"), all = T)
head(ex1.merge)

합쳐진 원래 데이터를 얻을 수 있다. all = T 는 한 쪽에만 있는 샘플을 유지하는 옵션이며 빈 변수는 NA 로 채워진다. 공통인 샘플만 취하려면 all = F 로 바꾸자.

마치며

이번 강의를 정리하자.

  1. RStudio cloud 로 클라우드 환경에서 실습을 진행했으며

  2. 기초 벡터연산과 for, if, ifelse, 함수만들기, apply 문을 통해 기본 문법을 익혔고

  3. 공단 검진 데이터를 실습자료를 읽어와 데이터를 살펴보는 법을 배웠다.

    • 변수 생성, 클래스 설정, 결측치 처리, 서브데이터, 그룹별 통계, 정렬

  4. 마지막으로 Long/wide type 데이터 변환과 merge 를 다루었다.

기타 기본적으로 알아야 할 R 명령어는 아래의 Base R Cheat Sheet 에서 확인할 수 있다.


다음 강의에서는 쉬운 문법으로 R 의 대세가 된 tidyverse 를 다룰 예정인데, 오늘 배운 기본 문법과 많은 비교가 될 것이다. 미리 알아보고 싶은 분은 본 블로그의 이전 글4 을 참고하기 바란다.

Footnotes

  1. https://jinseob2kim.github.io/rbasic.html↩︎

  2. https://jinseob2kim.github.io/radv1.html↩︎

  3. https://t1.daumcdn.net/cfile/tistory/2433F13D55E1163907↩︎

  4. https://blog.zarathu.com/posts/2019-01-03-rdatamanagement↩︎

Citation

BibTeX citation:
@online{kim2020,
  author = {Kim, Jinseob},
  title = {R {데이터} {매니지먼트:} {기초}},
  date = {2020-03-10},
  url = {https://blog.zarathu.com/jp/posts/2020-02-16-rdatamanagement-basic},
  langid = {en}
}
For attribution, please cite this work as:
Kim, Jinseob. 2020. “R 데이터 매니지먼트: 기초.” March 10, 2020. https://blog.zarathu.com/jp/posts/2020-02-16-rdatamanagement-basic.