시작하면서
본 내용은 필자가 준비하던 박사논문 선형모형의 다차원공간으로의 확장 의 후속으로 계획했던 내용으로, 선형모형 벡터공간에 허수축(Imaginary Axis) 을 도입, Inverted U-shape 을 선형관계로 재해석하였습니다. 아인슈타인 일반상대성이론의 4차원 시공간 중, 시간을 허수축으로 해석하는 것에서 아이디어를 얻었습니다. 이전 내용 의 요약은 아래 슬라이드를 참고해 주세요.
Abstract
이전 연구 에서 저자는 선형모형을 휘어진 다차원공간으로 확장하여 \(U\)-shaped relationship을 선형모형으로 해석하는 방법을 제시하였는데, Inverted \(U\)-shape은 이 방법으로 표현할 수 없었다. 이에 본 연구에서는 선형모형의 무대를 Imaginary Axis를 포함한 다차원공간까지 확장하여 Inverted \(U\)-shaped relationship을 선형모형으로 해석하는 방법을 제안한다. 본 연구를 활용하여 Health science 연구자들이 새로운 관점에서 연구데이터를 해석할 수 있을 것이다.
keywords : Multidimension, Linear Model, Vector Space, Metric Tensor
Introduction
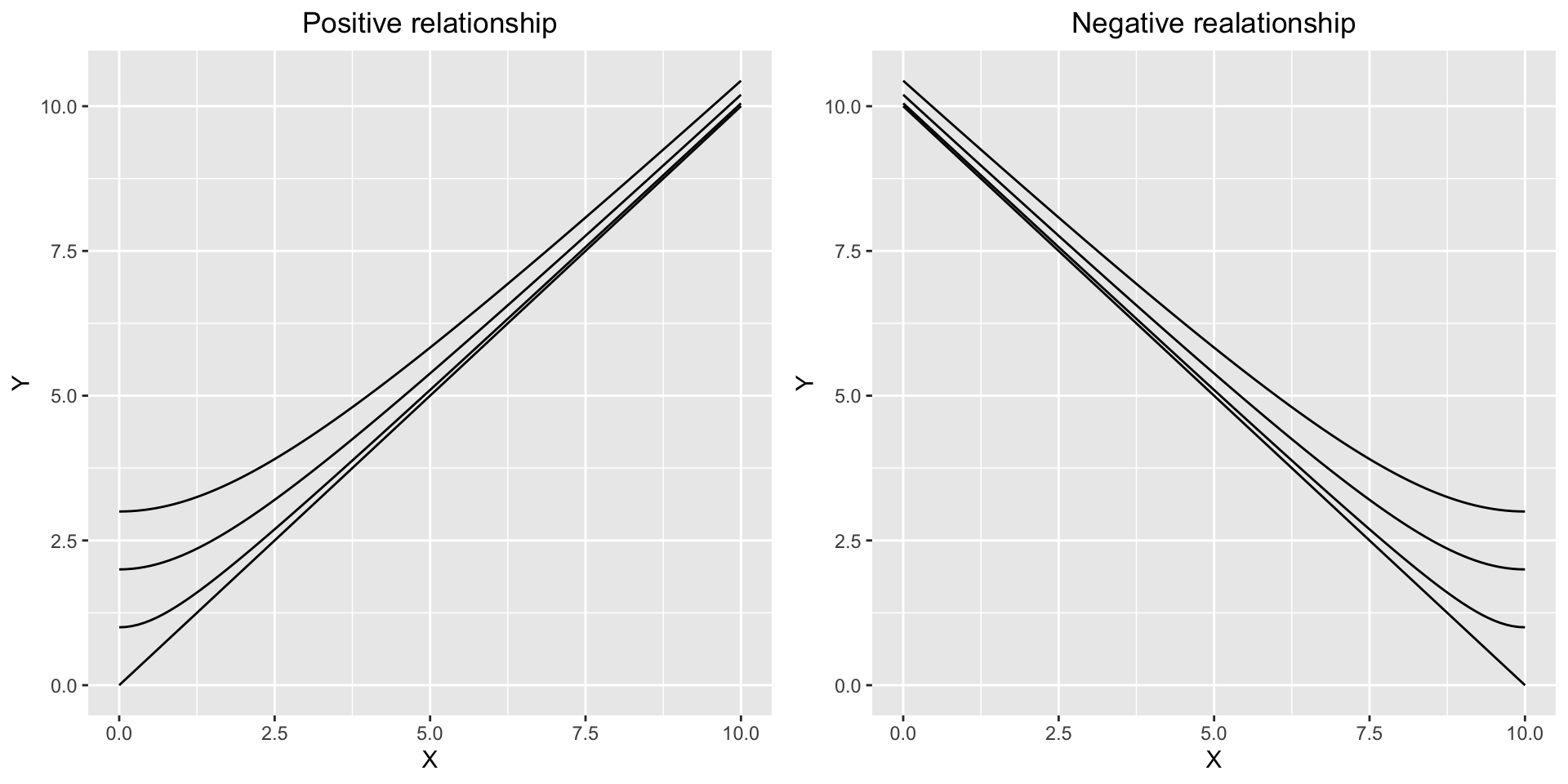
이전 연구에서 선형모형을 다차원 벡터공간으로 확장한 Multidimensional Vectorized Linear Model(MDVLM)을 제안하였는데, 변수들간의 dependency를 적절하게 조절하여 기존 선형모형에서 정확히 표현하기 어려웠던 관계를 표현할 수 있었다(Jinseob Kim 2017). 특히 MDVLM을 통해 점점 느리게 감소하는 혹은 점점 빠르게 증가하는 모양을 표현할 수 있는데, 이는 MDVLM의 표현식 \(Y^2= \beta_1^2X_1^2 + 2r\beta_1\beta_2X_1X_2+ \beta_2^2X_2^2 = (\beta_1X_1+r\beta_2X_2)^2 + (1-r^2)\beta_2^2X_2^2\)에서 \(X_1\)과 \(Y\)의 관계가 쌍곡선 모양을 보이기 때문이다(Figure 1).
이제 자연스러운 질문이 생긴다. “MDVLM은 점점 빠르게 감소하는 혹은 느리게 증가하는 관계를 표현할 수 있을까?” \(Y^2=X_1^2 - X_2^2\)의 간단한 예를 통해 이를 살펴보도록 하자.
Linear relationship can’t explained via MDVLM
\(Y^2 = X_1^2 - X_2^2\)의 그래프(\(X, Y > 0\))를 살펴보면 \(Y\)와 \(X_2\)는 타원모양(이 예시에서는 원)으로 감소하는 관계를 보이고 MDVLM으로 잘 표현할 수 없다(Figure 2(a)). MDVLM은 직선 혹은 쌍곡선 모양만 표현할 수 있기 때문이다.
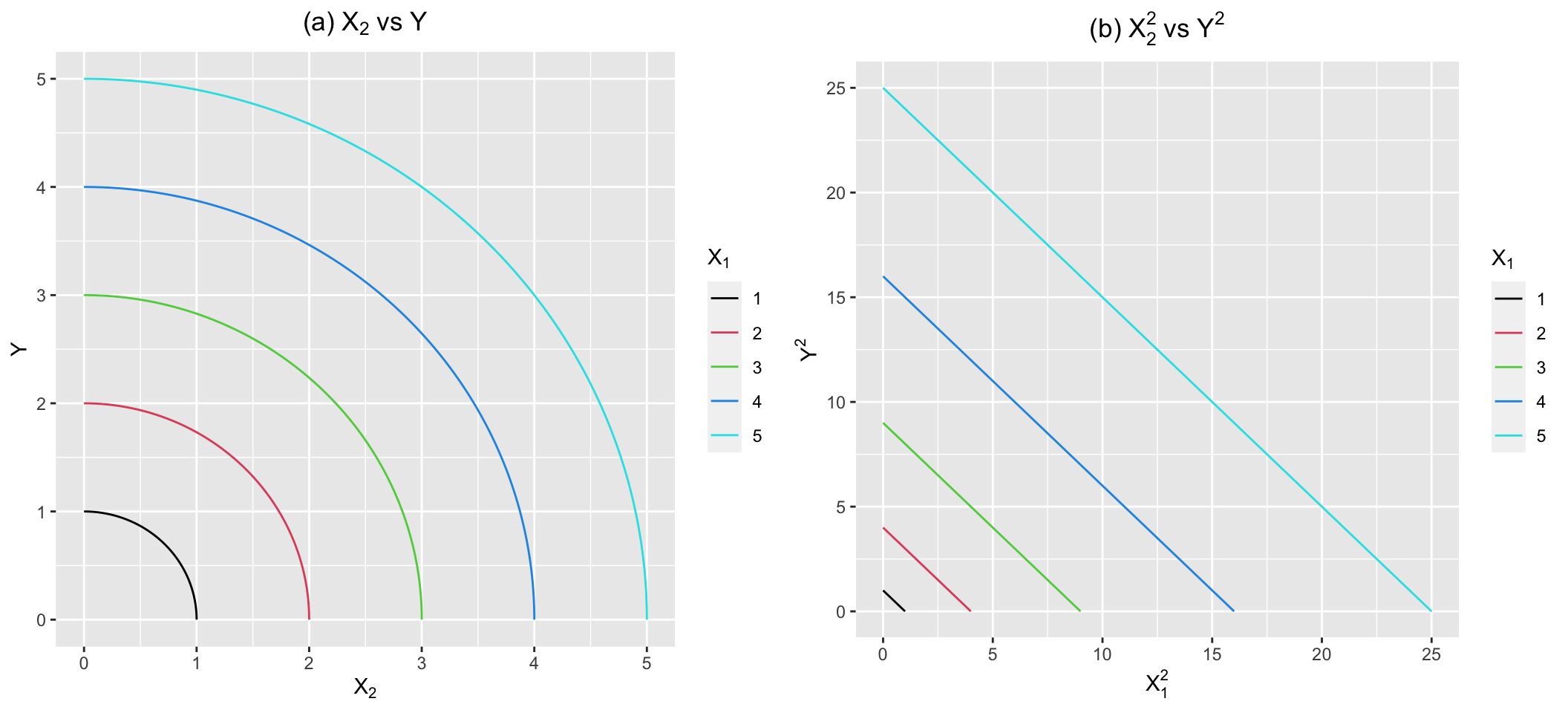
즉, \(Y^2 = X_1^2 - X_1^2\) 간단한 표현임에도 불구하고, 선형모형을 벡터공간으로 일반화한 MDVLM으로도 잘 표현될 수 없다. 그렇다면 이것은 선형모형이 아닌 것일까? 분명히 점점 빠르게 감소하는 타원 모양은 선형관계가 아니다. 그러나 \(X_2^2\)이 1 증가할 때 마다 \(Y^2\)가 정확히 1이 감소하는 관계가 있는 것도 사실이다(Figure 2(b)). 이 또한 선형관계라고 할 수 있는 것 아닐까?
이를 확인해 보기 위해 MDVLM에서와 마찬가지로 다차원 벡터공간에서 \(Y^2 = X_1^2 - X_2^2\)을 표현해보자.
\[\vec{Y} = \vec{X_1} + \vec{X_2}\]
\(\vec{X_1}\)와 \(\vec{X_2}\)가 독립된 axis를 갖고 있다면 \(Y^2 = \vec{Y}\cdot\vec{Y} = X_1^2 + X_2^2\)을 얻는다. 한편 \(\vec{X_2}\)가 허수축(imaginar axis)를 갖고 있다고 생각하면 아래와 같이 \(Y^2 = X_1^2 - X_2^2\)을 얻는다.
\[Y^2 = \vec{Y}\cdot\vec{Y} = X_1^2 + (iX_2)^2 = X_1^2 - X_2^2\]
이 경우에도 \(X_1\)이 고정된 상태에서는 \(\vec{Y}\)의 변화량 \(d\vec{Y}= d\vec{X_2}\)가 성립하며, 방향과 허수축을 고려했을 때 \(dY\)와 \(dX_2\)은 선형관계가 있다고 할 수 있다.
허수 \(i\)는 실제로 존재하는 것이 아니지만 \(i^2 = -1\)임을 이용해서 내적이 음수인 허수축을 상상할 수 있고, 선형관계를 허수축을 포함한 벡터공간으로 확장할 수 있다. 허수축의 활용은 물리학에서 많이 볼 수 있는데, 대표적으로 아인슈타인의 특수상대성이론에서는 time coordinate를 허수축으로 두고 4차원 시공간(Minkowski space)에서의 거리 \(ds\)를 아래와 같이 정의한다(Corry 1997).
\[(ds)^2 = (dx)^2 + (dy)^2 + (dz)^2 + (idt)^2 = (dx)^2 + (dy)^2 + (dz)^2 - (dt)^2\]
일반적으로 \(p\)개의 실수축과 \(q\)개의 허수축으로 구성된 manifold를 pseudo-Riemannian manifolds라 하고 거리 \(g\)는 아래와 같이 정의한다(Kulkarni 1981).
\[g = dx_1^2 + \cdots + dx_p^2 - dx_{p+1}^2 - \cdots - dx_{p+q}^2\]
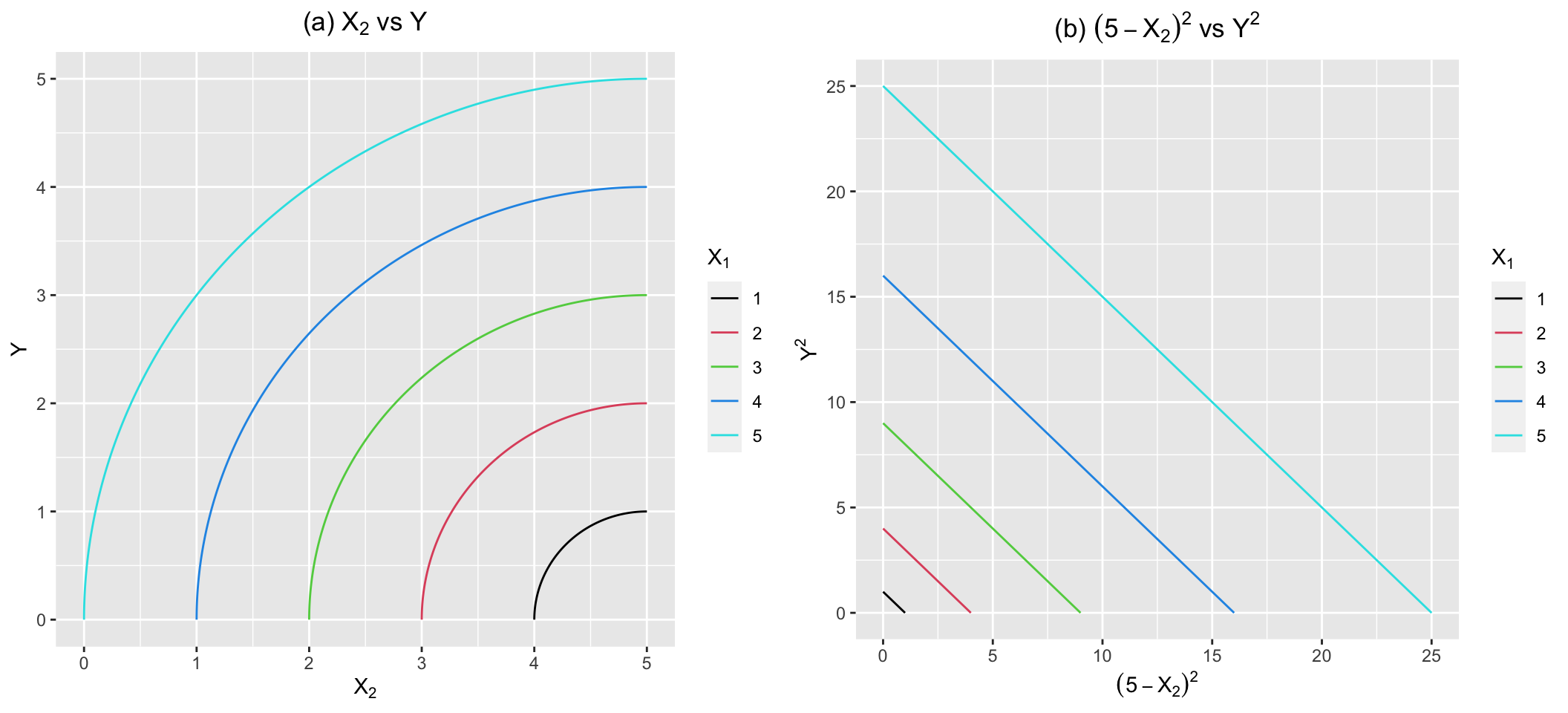
점점 느리게 증가하는 타원모양도 마찬가지로 MDVLM으로는 표현하기 어려우며 \(Y^2 = X_1^2 - (5-X_2)^2\)인 원을 예로 들 수 있다(Figure 3(a), 3(b)).
제안: MDVLM with Imaginary Axis
지금까지의 고찰을 토대로 본 연구에서는 허수축을 포함한 다차원 벡터공간에서 선형관계를 표현하는 MDVLM with Imaginary Axis(MDVLM-IA)를 제안한다. 이것은 기존의 MDVLM에 Imaginary Axis의 개념을 추가하여 일반화한 것인데, MDVLM의 개념을 간단하게 리뷰한 후 여기에 허수축을 추가하여 본 연구의 모형과 추정방법을 설명하겠다. 그 후 몇 가지 example을 통해 이것이 어떻게 활용되는지 살펴볼 것이다.
Formula
이전에 연구했던 MDVLM에 대해 간단히 리뷰를 한 후, 이것을 확장하여 본 연구의 모형과 추정을 설명하도록 하겠다.
Brief Review of MDVLM
음이 아닌 실수 \(Y\)와 \(X_1\), \(X_2\),\(\cdots\), \(X_n\) 들의 선형관계를 벡터공간에서 표현하면 아래와 같다.
\[\vec{Y} = (\beta_1X_1+\beta_{01})\vec{e_1}+ (\beta_2X_2+\beta_{02})\vec{e_2} + \cdots + (\beta_pX_p+\beta_{0p})\vec{e_p}\]
이 때, \(\vec{e_i}\)들은 \(X_i\)방향으로의 단위벡터로서 크기는 모두 1이며, \(X_i\)와 \(X_j\)가 완전히 독립적인 정보라면 \(\vec{e_i}\cdot\vec{e_j} = 0\)이고 일반적으로 \(r_{ij} = r_{ji} = \vec{e_i}\cdot\vec{e_j}\)의 값은 0에서 1까지의 값을 갖는다.
한편 \(\vec{Y}\)의 변화량 \(d\vec{Y}\)는
\[d\vec{Y} = \beta_1dX_1\vec{e_1} + \beta_2dX_2\vec{e_2} + \cdots + \beta_pdX_p\vec{e_p}\]
이며 \(\dfrac{\partial\vec{Y}}{\partial X_i} = \beta_i\vec{e_i}\)가 된다. 이는 \(X_i\)만 변하고 나머지는 고정되어 있을 때 \(\vec{Y}\)는 \(X_i\)의 방향(\(\vec{e_i}\))으로 \(\beta_i\)만큼 증가한다고 해석할 수 있고, 기존의 선형모형의 해석에 vector의 개념만 추가된 것이다.
\(\beta\)값들의 추정은 다음과 같은 스칼라식을 토대로 이루어진다.
\[ \begin{aligned} Y^2 = (\vec{Y})\cdot(\vec{Y}) &= (\sum_{i=1}^{p}(\beta_iX_i+\beta_{i0})\vec{e_i})\cdot (\sum_{i=1}^{p}(\beta_iX_i+\beta_{i0})\vec{e_i}) \\ &=\sum_{i=1}^p(\beta_iX_i+\beta_{i0})^2 + 2\sum_{i<j}r_{ij}(\beta_iX_i+\beta_{i0})(\beta_jX_j+\beta_{j0})\\ \end{aligned} \]
이제 최소제곱추정을 위한 오차제곱의 합(Sum of Squared Error: SSE)을 다음과 같이 정의하면, 기존 선형모형의 최소제곱추정을 자연스럽게 확장한 것이 된다.
\[SSE(\beta) = \sum_{k=1}^N (Y_k - \sqrt{\sum_{i=1}^n(\beta_iX_{ki}+\beta_{i0})^2 + 2\sum_{i<j}r_{ij}(\beta_iX_{ki}+\beta_{i0})(\beta_jX_{kj}+\beta_{j0})})^2\]
(\(Y_k, X_{ki}\): \(k\)th individual’s \(Y, X_{i}\) value)
예를 들어 \(r_{ij}\)가 전부 1이라면 \(SSE(\beta) = \sum_{k=1}^N (Y_k- \beta_0 -\beta_1X_{k1} - \beta_2X_{k2} - \cdots - \beta_pX_{kp})^2\)로 기존 선형모형의 최소제곱추정과 동일한 것을 확인할 수 있다.
\(SSE(\beta)\)를 최소로 하는 \(\beta\)값은 optimization technique를 이용하며, Nelder-Mead, BFGS, CG, L-BFGS-B 등 다양한 방법이 있다Nelder and Mead (1965).
MDVLM with Imaginary Axis
MDVLM에서 허수축을 갖는 \(X_{p+1}\),\(\cdots\),\(X_{p+q}\)를 추가하여 선형관계를 벡터공간에서 표현하면 아래와 같다.
\[\vec{Y} = (\beta_1X_1+\beta_{01})\vec{e_1}+ \cdots + (\beta_pX_p+\beta_{0p})\vec{e_p} + (\beta_{p+1}X_{p+1}+\beta_{0(p+1)})\vec{e_{p+1}} + \cdots + (\beta_{p+q}X_{p+q}+\beta_{0(p+q)})\vec{e_{p+q}}\]
\(\vec{e_1},\cdots,\vec{e_p}\)들은 실수축을 가진 단위벡터로서 자기자신과의 내적값인 \(\vec{e_i}\cdot\vec{e_i}\)의 값이 1 이다. 반면 \(\vec{e_{p+1}},\cdots,\vec{e_{p+q}}\)는 허수축을 가진 단위벡터로서 자기자신과의 내적값은 -1이다. \(1\le i, j \le p\)일 때는 \(r_{ij} = r_{ji} = \vec{e_i}\cdot\vec{e_j}\)가 0에서 1까지의 값을 갖으며, \(p+1\le i, j \le p+q\)라면 -1에서 0까지의 값을 갖고, 그 외에는 \(r_{ij}=0\)이다. 즉 Axis들의 dependency는 실수축끼리, 혹은 허수축끼리만 정의한다.
\(\vec{Y}\)의 변화량 \(d\vec{Y}\)는
\[d\vec{Y} = \beta_1dX_1\vec{e_1} + \cdots + \beta_pdX_p\vec{e_p} + \beta_{p+1}dX_{p+1}\vec{e_{p+1}} + \cdots + \beta_{p+q}dX_{p+q}\vec{e_{p+q}}\]
이며 \(\dfrac{\partial\vec{Y}}{\partial X_i} = \beta_i\vec{e_i}\)가 된다. 이는 \(X_i\)만 변하고 나머지는 고정되어 있을 때 \(\vec{Y}\)는 \(X_i\)의 방향(\(\vec{e_i}\))으로 \(\beta_i\)만큼 증가한다고 해석할 수 있고 이는 MDVLM에서의 해석과 동일하다.
추정을 위한 스칼라 관계식은 MDVLM때와 비슷하게 아래와 같이 표현할 수 있다.
\[ \begin{aligned} Y^2 &= (\sum_{i=1}^{p}(\beta_iX_i+\beta_{0i})\vec{e_i} + \sum_{i=p+1}^{p+q}(\beta_iX_i+\beta_{0i})\vec{e_i})\cdot (\sum_{i=1}^{p}(\beta_iX_i+\beta_{0i})\vec{e_i} + \sum_{i=p+1}^{p+q}(\beta_iX_i+\beta_{0i})\vec{e_i}) \\ &=(\sum_{i=1}^p(\beta_iX_i+\beta_{0i})^2 + \sum_{1\le i<j \le p}2r_{ij}(\beta_iX_i+\beta_{0i})(\beta_jX_j+\beta_{0j})) - (\sum_{i=p+1}^{p+q}(\beta_iX_i+\beta_{0i})^2 + \sum_{p< i<j\le p+q}2r_{ij}(\beta_iX_i+\beta_{0i})(\beta_jX_j+\beta_{0j}))\\ \end{aligned} \] \(Y\)의 값의 변화량 \(dY\)는 \[ \begin{aligned} (dY)^2 &= (\sum_{i=1}^{p}\beta_idX_i\vec{e_i} + \sum_{i=p+1}^{p+q}\beta_idX_i\vec{e_i})\cdot (\sum_{i=1}^{p}\beta_idX_i\vec{e_i} + \sum_{i=p+1}^{p+q}\beta_idX_i\vec{e_i}) \\ &=(\sum_{i=1}^p\beta_i^2(dX_i)^2 + \sum_{1 \le i<j \le p}2r_{ij}\beta_i\beta_jdX_idX_j) - (\sum_{i=p+1}^{p+q}\beta_i^2(dX_i)^2 + \sum_{p < i<j \le p+q}2r_{ij}\beta_i\beta_jdX_idX_j)\\ \end{aligned} \]
이고, 모든 \(r_{ij}\)들이 0이라면 \(\sum_{i=1}^p\beta_i^2(dX_i)^2 - \sum_{i=p+1}^{p+q}\beta_i^2(dX_i)^2\)로 간단히 표현할 수 있다.
최소제곱 추정을 위한 \(SSE(\beta)\)값도 비슷하게 정의할 수 있으며 추정방법은 MDVLM의 경우와 같이 optimization technique를 이용한다.
\[
\begin{aligned}
f(\beta,X_k) &= (\sum_{i=1}^p(\beta_iX_{ki}+\beta_{0i})^2 + \sum_{1\le i<j \le p}2r_{ij}(\beta_iX_{ki}+\beta_{0i})(\beta_jX_{kj}+\beta_{0j})) - (\sum_{i=p+1}^{p+q}(\beta_iX_{ki}+\beta_{0i})^2 + \sum_{p< i<j\le p+q}2r_{ij}(\beta_iX_{ki}+\beta_{0i})(\beta_jX_{kj}+\beta_{0j})) \\
SSE(\beta) &= \sum_{k=1}^N (Y_k - \sqrt{f(\beta,X_k)})^2
\end{aligned}
\]
(\(Y_k, X_{ki}\): \(k\)th individual’s \(Y, X_{i}\) value, \(X_k= (X_{k1},\cdots,X_{k(p+q)})\))
Apply to Data
앞서 언급했던 \(Y^2 = X_1^2 - X_2^2\)과 \(Y^2 = X_1^2 - (5-X_2)^2\)인 경우의 데이터에 적용해보도록 하겠다. 모든 계산은 R 3.3.3의 optim 함수를 이용하였다.
Example 1: \(Y^2 = X_1^2 - X_2^2\)
\(Y^2 = X_1^2 - X_2^2\)인 양수 \(Y, X_1, X_2\)의 쌍을 100번 random sampling 해서 MDVLM과 본 연구의 모형을 비교해 보았다.
| Best Scenario of MDVLM | MDVLM-IA | |
|---|---|---|
| Formula | \(Y^2 = (-0.224 + 1.163X_1 -0.634X_2)^2\) | \(Y^2 = X_1^2 -X_2^2\) |
| MSE | 0.176 | 0 |
실제로 \(Y^2\)과 \(X_1^2, X_2^2\)의 값을 이용해서 선형모형으로 추정하면 정확한 추정 결과를 얻는다. 그러나 제곱한 값이 아닌 원래값을 이용해서 선형모형에 적용하면 \(Y =\) \(-0.224\) \(+\) \(1.163\) \(X_1 +\) \(-0.634\) \(X_2\)이 되어 정확한 추정을 얻지 못하고, MDVLM으로 확장해도 이보다 정확한 추정은 얻을 수 없다.
Example 2: \(Y^2 = X_1^2 - (5-X_2)^2\)
| Best Scenario of MDVLM | MDVLM-IA | |
|---|---|---|
| Formula | \(Y^2 = (-2.78 + 1.079X_1 + 0.567X_2)^2\) | \(Y^2 = X_1^2 - (5-X_2)^2\) |
| MSE | 0.047 | 0 |
Discussion
예상대로 \(Y\)가 빨리 감소하거나 천천히 증가하는 타원모양의 관계는 MDVLM으로 잘 표현할 수 없었으며, 허수축을 활용했을 때 정확히 표현할 수 있었다.
본 연구가 Health Status를 설명하기 위해 처음으로 허수 \(i\)의 개념을 이용하였다는 의의가 있다. 본 연구에서는 \(i^2 = -1\)이라는 특징을 이용해서 타원모양을 허수축에서의 선형관계로 재해석하여 MDVLM보다 더 확장된 선형모형을 제시하였는데, 이를 통해 연구자들이 선형관계라는 직관적 해석을 잃지 않으면서 지금보다 훨씬 다양하게 건강현상을 설명할 수 있을 것이라 확신한다.
허수 \(i\)의 또하나의 큰 특징은 복소수 표현을 통해 실수체계를 확장할 수 있다는 것인데, 이것을 적극적으로 활용한 분야 중 하나가 양자역학이다. 양자역학의 대표적인 방정식인 슈뢰딩거 방정식(Schrödinger equation)은 입자의 운동은 확률로 기술되고 그 확률은 파동처럼 행동한다는 내용인데 파동을 기술하는 함수가 복소수로 표현되어 있다는 것이 특징이며, 복소수가 포함된 파동함수 그 자체로는 실제 세계를 해석하기 어렵지만 켤레복소수와의 곱을 통해 확률을 표현할 수 있다. 양자역학이 미시세계의 현상을 설명하는 새로운 방법이 된 것과 마찬가지로 확률을 복소수를 포함한 파동함수로 표현하는 방법이 향후 Health science에서 건강상태를 설명하는 새로운 방법이 될 수 있을 것이라 예상한다.
본 연구를 시작으로 향후 Health science에서 복소수를 활용한 모형이 활발히 제안되길 기대한다.
References
Citation
@online{kim2019,
author = {Kim, Jinseob},
title = {선형모형의 {다차원공간으로의} {확장(2):} {허수축} {도입}},
date = {2019-08-14},
url = {https://blog.zarathu.com/posts/2019-08-14-mdlmwithimaginaryaxes},
langid = {en}
}